Graph Data Structure is a non-linear data structure consisting of vertices and edges. It is useful in fields such as social network analysis, recommendation systems, and computer networks. In the field of sports data science, graph data structure can be used to analyze and understand the dynamics of team performance and player interactions on the field.
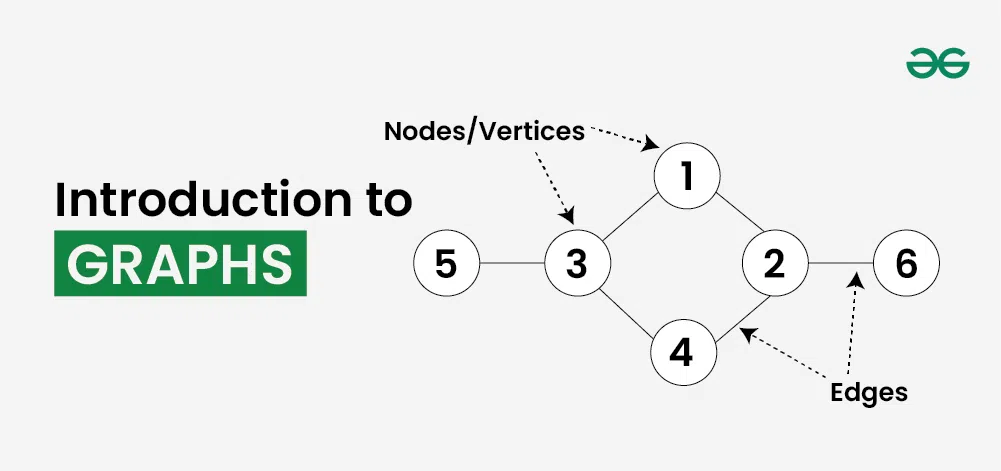
Table of Content
- What is Graph Data Structure?
- Components of Graph Data Structure
- Types Of Graph Data Structure
- Representation of Graph Data Structure
- Basic Operations on Graph Data Structure
- Difference between Tree and Graph
- Real-Life Applications of Graph Data Structure
- Advantages of Graph Data Structure
- Disadvantages of Graph Data Structure
- Frequently Asked Questions(FAQs) on Graph Data Structure
What is Graph Data Structure?
Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E).
Imagine a game of football as a web of connections, where players are the nodes and their interactions on the field are the edges. This web of connections is exactly what a graph data structure represents, and it's the key to unlocking insights into team performance and player dynamics in sports.
Components of Graph Data Structure
- Vertices: Vertices are the fundamental units of the graph. Sometimes, vertices are also known as vertex or nodes. Every node/vertex can be labeled or unlabelled.
- Edges: Edges are drawn or used to connect two nodes of the graph. It can be ordered pair of nodes in a directed graph. Edges can connect any two nodes in any possible way. There are no rules. Sometimes, edges are also known as arcs. Every edge can be labelled/unlabelled.
Types Of Graph Data Structure:
1. Null Graph
A graph is known as a null graph if there are no edges in the graph.
2. Trivial Graph
Graph having only a single vertex, it is also the smallest graph possible. 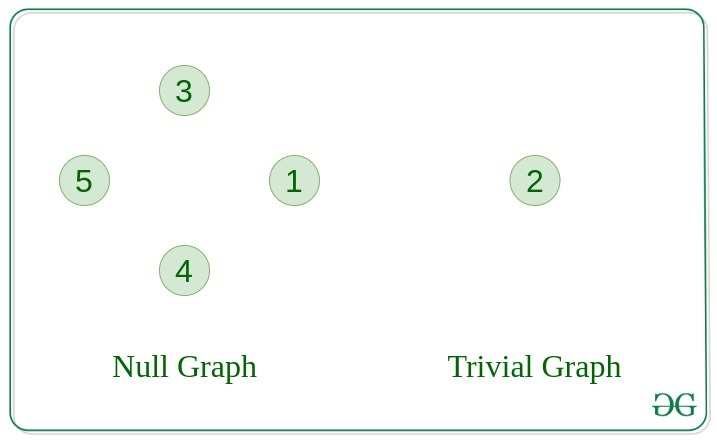
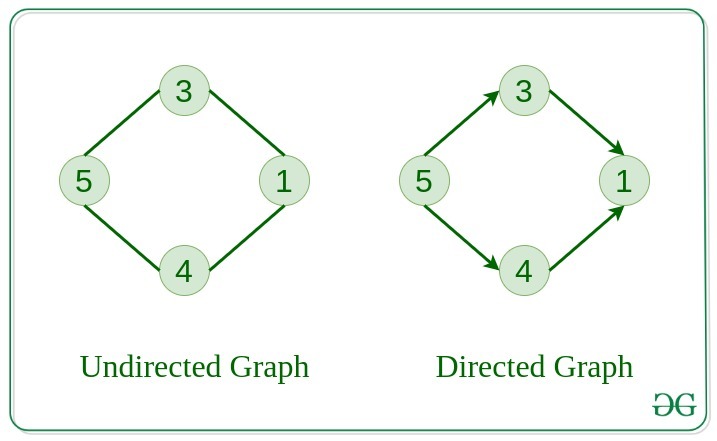
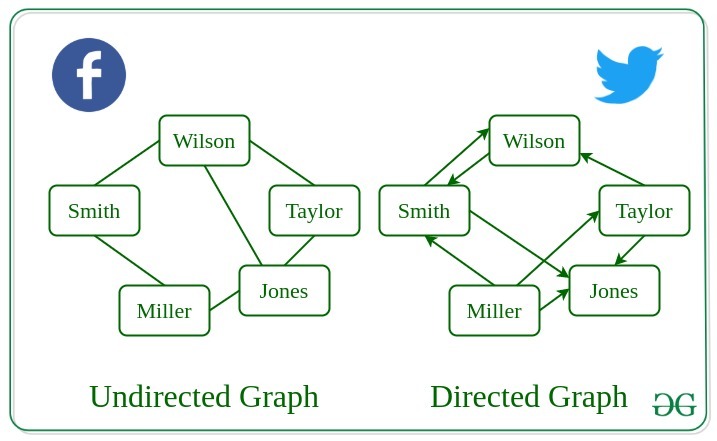
3. Undirected Graph
A graph in which edges do not have any direction. That is the nodes are unordered pairs in the definition of every edge.
4. Directed Graph
A graph in which edge has direction. That is the nodes are ordered pairs in the definition of every edge.
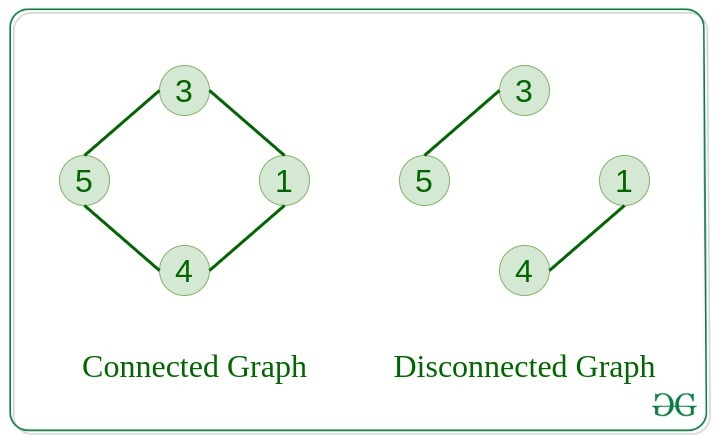
5. Connected Graph
The graph in which from one node we can visit any other node in the graph is known as a connected graph.
6. Disconnected Graph
The graph in which at least one node is not reachable from a node is known as a disconnected graph.
7. Regular Graph
The graph in which the degree of every vertex is equal to K is called K regular graph.
8. Complete Graph
The graph in which from each node there is an edge to each other node. 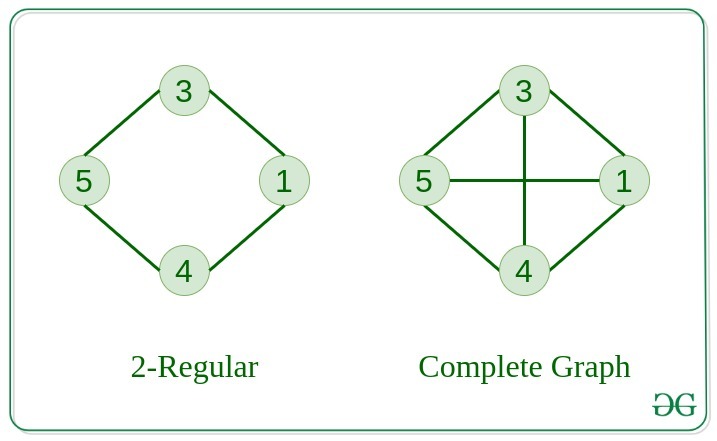
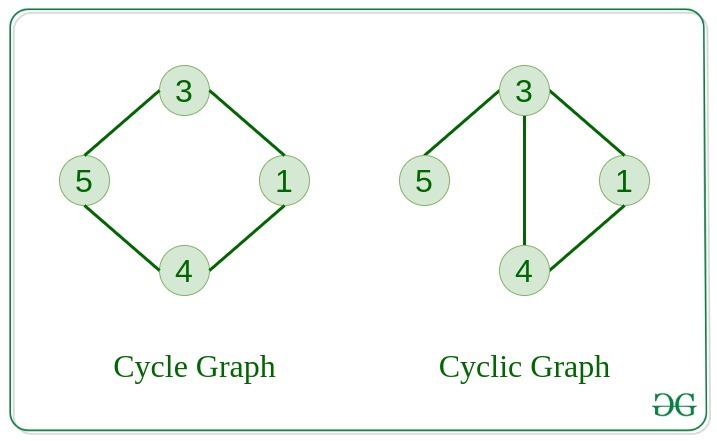
9. Cycle Graph
The graph in which the graph is a cycle in itself, the degree of each vertex is 2.
10. Cyclic Graph
A graph containing at least one cycle is known as a Cyclic graph.
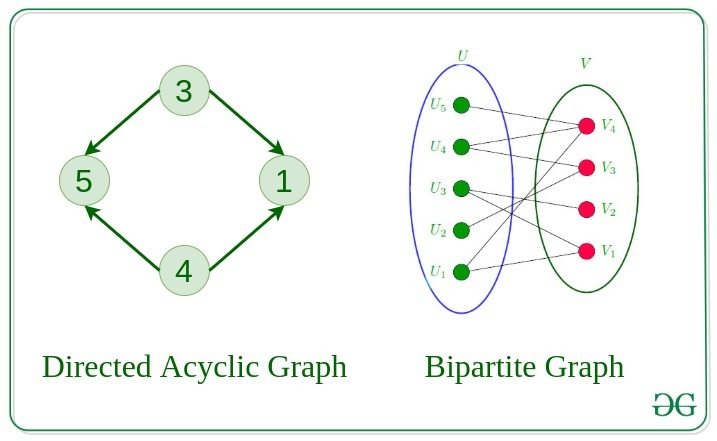
11. Directed Acyclic Graph
A Directed Graph that does not contain any cycle.
12. Bipartite Graph
A graph in which vertex can be divided into two sets such that vertex in each set does not contain any edge between them.
13. Weighted Graph
- A graph in which the edges are already specified with suitable weight is known as a weighted graph.
- Weighted graphs can be further classified as directed weighted graphs and undirected weighted graphs.
Representation of Graph Data Structure:
There are two ways to store a graph:
- Adjacency Matrix
- Adjacency List
Adjacency Matrix Representation of Graph Data Structure:
In this method, the graph is stored in the form of the 2D matrix where rows and columns denote vertices. Each entry in the matrix represents the weight of the edge between those vertices.
-copy.webp)
Below is the implementation of Graph Data Structure represented using Adjacency Matrix:
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int> >
createAdjacencyMatrix(vector<vector<int> >& graph,
int numVertices)
{
// Initialize the adjacency matrix with zeros
vector<vector<int> > adjMatrix(
numVertices, vector<int>(numVertices, 0));
// Fill the adjacency matrix based on the edges in the
// graph
for (int i = 0; i < numVertices; ++i) {
for (int j = 0; j < numVertices; ++j) {
if (graph[i][j] == 1) {
adjMatrix[i][j] = 1;
adjMatrix[j][i]
= 1; // For undirected graph, set
// symmetric entries
}
}
}
return adjMatrix;
}
int main()
{
// The indices represent the vertices, and the values
// are lists of neighboring vertices
vector<vector<int> > graph = { { 0, 1, 0, 0 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 0, 0, 1, 0 } };
int numVertices = graph.size();
// Create the adjacency matrix
vector<vector<int> > adjMatrix
= createAdjacencyMatrix(graph, numVertices);
// Print the adjacency matrix
for (int i = 0; i < numVertices; ++i) {
for (int j = 0; j < numVertices; ++j) {
cout << adjMatrix[i][j] << " ";
}
cout << endl;
}
return 0;
}
import java.util.ArrayList;
import java.util.Arrays;
public class AdjacencyMatrix {
public static int[][] createAdjacencyMatrix(
ArrayList<ArrayList<Integer> > graph,
int numVertices)
{
// Initialize the adjacency matrix with zeros
int[][] adjMatrix
= new int[numVertices][numVertices];
// Fill the adjacency matrix based on the edges in
// the graph
for (int i = 0; i < numVertices; ++i) {
for (int j = 0; j < numVertices; ++j) {
if (graph.get(i).get(j) == 1) {
adjMatrix[i][j] = 1;
adjMatrix[j][i]
= 1; // For undirected graph, set
// symmetric entries
}
}
}
return adjMatrix;
}
public static void main(String[] args)
{
// The indices represent the vertices, and the
// values are lists of neighboring vertices
ArrayList<ArrayList<Integer> > graph
= new ArrayList<>();
graph.add(
new ArrayList<>(Arrays.asList(0, 1, 0, 0)));
graph.add(
new ArrayList<>(Arrays.asList(1, 0, 1, 0)));
graph.add(
new ArrayList<>(Arrays.asList(0, 1, 0, 1)));
graph.add(
new ArrayList<>(Arrays.asList(0, 0, 1, 0)));
int numVertices = graph.size();
// Create the adjacency matrix
int[][] adjMatrix
= createAdjacencyMatrix(graph, numVertices);
// Print the adjacency matrix
for (int i = 0; i < numVertices; ++i) {
for (int j = 0; j < numVertices; ++j) {
System.out.print(adjMatrix[i][j] + " ");
}
System.out.println();
}
}
}
// This code is contributed by shivamgupta310570
def create_adjacency_matrix(graph):
# Get the number of vertices in the graph
num_vertices = len(graph)
# Initialize the adjacency matrix with zeros
adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]
# Fill the adjacency matrix based on the edges in the graph
for i in range(num_vertices):
for j in range(num_vertices):
if graph[i][j] == 1:
adj_matrix[i][j] = 1
# For undirected graph, set symmetric entries
adj_matrix[j][i] = 1
return adj_matrix
# The indices represent the vertices, and the values are lists of neighboring vertices
graph = [
[0, 1, 0, 0],
[1, 0, 1, 0],
[0, 1, 0, 1],
[0, 0, 1, 0]
]
# Create the adjacency matrix
adj_matrix = create_adjacency_matrix(graph)
# Print the adjacency matrix
for row in adj_matrix:
print(' '.join(map(str, row)))
# This code is contributed by shivamgupta0987654321
function createAdjacencyMatrix(graph) {
const numVertices = graph.length;
// Initialize the adjacency matrix with zeros
const adjMatrix = Array.from(Array(numVertices), () => Array(numVertices).fill(0));
// Fill the adjacency matrix based on the edges in the graph
for (let i = 0; i < numVertices; ++i) {
for (let j = 0; j < numVertices; ++j) {
if (graph[i][j] === 1) {
adjMatrix[i][j] = 1;
adjMatrix[j][i] = 1; // For undirected graph, set symmetric entries
}
}
}
return adjMatrix;
}
// The indices represent the vertices, and the values are lists of neighboring vertices
const graph = [
[0, 1, 0, 0],
[1, 0, 1, 0],
[0, 1, 0, 1],
[0, 0, 1, 0]
];
// Create the adjacency matrix
const adjMatrix = createAdjacencyMatrix(graph);
// Print the adjacency matrix
for (let i = 0; i < adjMatrix.length; ++i) {
console.log(adjMatrix[i].join(' '));
}
Adjacency List Representation of Graph:
This graph is represented as a collection of linked lists. There is an array of pointer which points to the edges connected to that vertex.
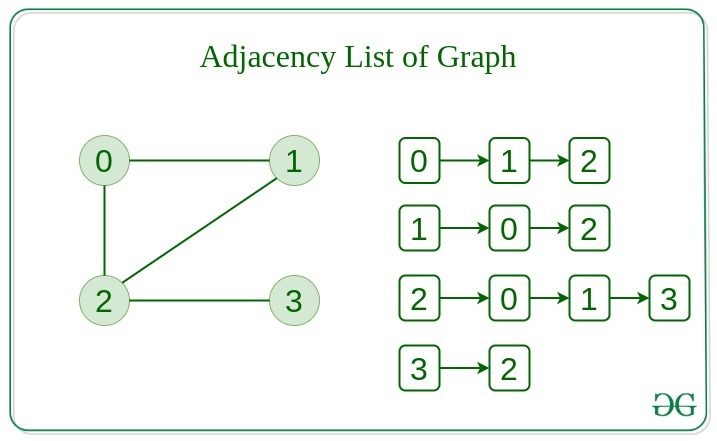
Below is the implementation of Graph Data Structure represented using Adjacency List:
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> createAdjacencyList(vector<vector<int> >& edges, int numVertices)
{
// Initialize the adjacency list
vector<vector<int> > adjList(numVertices);
// Fill the adjacency list based on the edges in the
// graph
for (int i=0; i < edges.size(); i++) {
int u = edges[i][0];
int v = edges[i][1];
// Since the graph is undirected, therefore we push the edges in both the directions
adjList[u].push_back(v);
adjList[v].push_back(u);
}
return adjList;
}
int main()
{
// Undirected Graph of 4 nodes
int numVertices = 4;
vector<vector<int>> edges = {{0, 1}, {0, 2}, {1, 2}, {2, 3}, {3, 1}};
// Create the adjacency List
vector<vector<int>> adjList = createAdjacencyList(edges, numVertices);
// Print the adjacency List
for (int i = 0; i < numVertices; ++i) {
cout << i << " -> ";
for (int j = 0; j < adjList[i].size(); ++j) {
cout << adjList[i][j] << " ";
}
cout << endl;
}
return 0;
}
import java.util.ArrayList;
import java.util.List;
public class Main {
public static List<List<Integer> >
createAdjacencyList(List<List<Integer> > edges,
int numVertices)
{
// Initialize the adjacency list
List<List<Integer> > adjList
= new ArrayList<>(numVertices);
for (int i = 0; i < numVertices; i++) {
adjList.add(new ArrayList<>());
}
// Fill the adjacency list based on the edges in the
// graph
for (List<Integer> edge : edges) {
int u = edge.get(0);
int v = edge.get(1);
// Since the graph is undirected, therefore we
// push the edges in both the directions
adjList.get(u).add(v);
adjList.get(v).add(u);
}
return adjList;
}
public static void main(String[] args)
{
// Undirected Graph of 4 nodes
int numVertices = 4;
List<List<Integer> > edges = new ArrayList<>();
edges.add(List.of(0, 1));
edges.add(List.of(0, 2));
edges.add(List.of(1, 2));
edges.add(List.of(2, 3));
edges.add(List.of(3, 1));
// Create the adjacency list
List<List<Integer> > adjList
= createAdjacencyList(edges, numVertices);
// Print the adjacency list
for (int i = 0; i < numVertices; ++i) {
System.out.print(i + " -> ");
for (int j = 0; j < adjList.get(i).size();
++j) {
System.out.print(adjList.get(i).get(j)
+ " ");
}
System.out.println();
}
}
}
def create_adjacency_list(edges, num_vertices):
# Initialize the adjacency list
adj_list = [[] for _ in range(num_vertices)]
# Fill the adjacency list based on the edges in the graph
for u, v in edges:
# Since the graph is undirected, push the edges in both directions
adj_list[u].append(v)
adj_list[v].append(u)
return adj_list
if __name__ == "__main__":
# Undirected Graph of 4 nodes
num_vertices = 4
edges = [(0, 1), (0, 2), (1, 2), (2, 3), (3, 1)]
# Create the adjacency list
adj_list = create_adjacency_list(edges, num_vertices)
# Print the adjacency list
for i in range(num_vertices):
print(f"{i} -> {' '.join(map(str, adj_list[i]))}")
using System;
using System.Collections.Generic;
class MainClass {
public static List<List<int> >
CreateAdjacencyList(List<List<int> > edges,
int numVertices)
{
// Initialize the adjacency list
List<List<int> > adjList
= new List<List<int> >(numVertices);
for (int i = 0; i < numVertices; i++) {
adjList.Add(new List<int>());
}
// Fill the adjacency list based on the edges in the
// graph
foreach(List<int> edge in edges)
{
int u = edge[0];
int v = edge[1];
// Since the graph is undirected, push the edges
// in both directions
adjList[u].Add(v);
adjList[v].Add(u);
}
return adjList;
}
public static void Main(string[] args)
{
// Undirected Graph of 4 nodes
int numVertices = 4;
List<List<int> > edges = new List<List<int> >{
new List<int>{ 0, 1 }, new List<int>{ 0, 2 },
new List<int>{ 1, 2 }, new List<int>{ 2, 3 },
new List<int>{ 3, 1 }
};
// Create the adjacency list
List<List<int> > adjList
= CreateAdjacencyList(edges, numVertices);
// Print the adjacency list
for (int i = 0; i < numVertices; i++) {
Console.Write($"{i} -> ");
foreach(int vertex in adjList[i])
{
Console.Write($"{vertex} ");
}
Console.WriteLine();
}
}
}
function createAdjacencyList(edges, numVertices) {
// Initialize the adjacency list
const adjList = new Array(numVertices).fill(null).map(() => []);
// Fill the adjacency list based on the edges in the graph
edges.forEach(([u, v]) => {
// Since the graph is undirected, push the edges in both directions
adjList[u].push(v);
adjList[v].push(u);
});
return adjList;
}
// Undirected Graph of 4 nodes
const numVertices = 4;
const edges = [[0, 1], [0, 2], [1, 2], [2, 3], [3, 1]];
// Create the adjacency list
const adjList = createAdjacencyList(edges, numVertices);
// Print the adjacency list
for (let i = 0; i < numVertices; i++) {
console.log(`${i} -> ${adjList[i].join(' ')}`);
}
Output
0 -> 1 2 1 -> 0 2 3 2 -> 0 1 3 3 -> 2 1
Comparison between Adjacency Matrix and Adjacency List
When the graph contains a large number of edges then it is good to store it as a matrix because only some entries in the matrix will be empty. An algorithm such as Prim's and Dijkstra adjacency matrix is used to have less complexity.
| Action | Adjacency Matrix | Adjacency List |
|---|---|---|
| Adding Edge | O(1) | O(1) |
| Removing an edge | O(1) | O(N) |
| Initializing | O(N*N) | O(N) |
Basic Operations on Graph Data Structure:
Below are the basic operations on the graph:
- Insertion or Deletion of Nodes in the graph
- Insertion or Deletion of Edges in the graph
- Searching in Graph Data Structure- Search an entity in the graph.
- Traversal of Graph Data Structure- Traversing all the nodes in the graph.
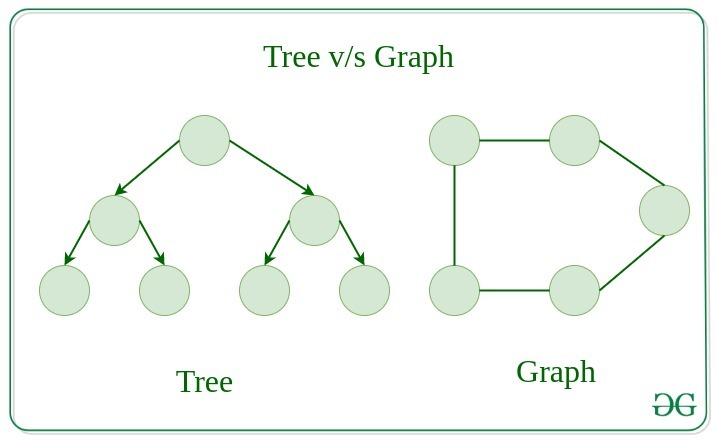
Difference between Tree and Graph:
Tree is a restricted type of Graph Data Structure, just with some more rules. Every tree will always be a graph but not all graphs will be trees. Linked List, Trees, and Heaps all are special cases of graphs.
Real-Life Applications of Graph Data Structure:
Graph Data Structure has numerous real-life applications across various fields. Some of them are listed below:
- Graph Data Structure is used to represent social networks, such as networks of friends on social media.
- It can be used to represent the topology of computer networks, such as the connections between routers and switches.
- It can used to represent the connections between different places in a transportation network, such as roads and airports.
- Neural Networks: Vertices represent neurons and edges represent the synapses between them. Neural networks are used to understand how our brain works and how connections change when we learn. The human brain has about 10^11 neurons and close to 10^15 synapses.
- Compilers: Graph Data Structure is used extensively in compilers. They can be used for type inference, for so-called data flow analysis, register allocation, and many other purposes. They are also used in specialized compilers, such as query optimization in database languages.
- Robot planning: Vertices represent states the robot can be in and the edges the possible transitions between the states. Such graph plans are used, for example, in planning paths for autonomous vehicles.
Advantages of Graph Data Structure:
- Graph Data Structure used to represent a wide range of relationships and data structures.
- They can be used to model and solve a wide range of problems, including pathfinding, data clustering, network analysis, and machine learning.
- Graph algorithms are often very efficient and can be used to solve complex problems quickly and effectively.
- Graph Data Structure can be used to represent complex data structures in a simple and intuitive way, making them easier to understand and analyze.
Disadvantages of Graph Data Structure:
- Graph Data Structure can be complex and difficult to understand, especially for people who are not familiar with graph theory or related algorithms.
- Creating and manipulating graphs can be computationally expensive, especially for very large or complex graphs.
- Graph algorithms can be difficult to design and implement correctly, and can be prone to bugs and errors.
- Graph Data Structure can be difficult to visualize and analyze, especially for very large or complex graphs, which can make it challenging to extract meaningful insights from the data.
Frequently Asked Questions(FAQs) on Graph Data Structure:
1. What is a graph?
A graph is a data structure consisting of a set of vertices (nodes) and a set of edges that connect pairs of vertices.
2. What are the different types of Graph Data Structure?
Graph Data Structure can be classified into various types based on properties such as directionality of edges (directed or undirected), presence of cycles (acyclic or cyclic), and whether multiple edges between the same pair of vertices are allowed (simple or multigraph).
3. What are the applications of Graph Data Structure?
Graph Data Structure has numerous applications in various fields, including social networks, transportation networks, computer networks, recommendation systems, biology, chemistry, and more.
4. What is the difference between a directed graph and an undirected graph?
In an undirected graph, edges have no direction, meaning they represent symmetric relationships between vertices. In a directed graph (or digraph), edges have a direction, indicating a one-way relationship between vertices.
5. What is a weighted graph?
A weighted graph is a graph in which each edge is assigned a numerical weight or cost. These weights can represent distances, costs, or any other quantitative measure associated with the edges.
6. What is the degree of a vertex in a graph?
The degree of a vertex in a graph is the number of edges incident to that vertex. In a directed graph, the indegree of a vertex is the number of incoming edges, and the outdegree is the number of outgoing edges.
7. What is a path in a graph?
A path in a graph is a sequence of vertices connected by edges. The length of a path is the number of edges it contains.
8. What is a cycle in a graph?
A cycle in a graph is a path that starts and ends at the same vertex, traversing a sequence of distinct vertices and edges in between.
9. What are spanning trees and minimum spanning trees?
A spanning tree of a graph is a subgraph that is a tree and includes all the vertices of the original graph. A minimum spanning tree (MST) is a spanning tree with the minimum possible sum of edge weights.
10. What algorithms are commonly used to traverse or search Graph Data Structure?
Common graph traversal algorithms include depth-first search (DFS) and breadth-first search (BFS). These algorithms are used to explore or visit all vertices in a graph, typically starting from a specified vertex. Other algorithms, such as Dijkstra's algorithm and Bellman-Ford algorithm, are used for shortest path finding.