Prim’s Algorithm for Minimum Spanning Tree (MST)
Last Updated :
16 Feb, 2024
Introduction to Prim’s algorithm:
We have discussed Kruskal’s algorithm for Minimum Spanning Tree. Like Kruskal’s algorithm, Prim’s algorithm is also a Greedy algorithm. This algorithm always starts with a single node and moves through several adjacent nodes, in order to explore all of the connected edges along the way.
The algorithm starts with an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, and the other set contains the vertices not yet included. At every step, it considers all the edges that connect the two sets and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST.
A group of edges that connects two sets of vertices in a graph is called cut in graph theory. So, at every step of Prim’s algorithm, find a cut, pick the minimum weight edge from the cut, and include this vertex in MST Set (the set that contains already included vertices).
How does Prim’s Algorithm Work?
The working of Prim’s algorithm can be described by using the following steps:
Step 1: Determine an arbitrary vertex as the starting vertex of the MST.
Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST (known as fringe vertex).
Step 3: Find edges connecting any tree vertex with the fringe vertices.
Step 4: Find the minimum among these edges.
Step 5: Add the chosen edge to the MST if it does not form any cycle.
Step 6: Return the MST and exit
Note: For determining a cycle, we can divide the vertices into two sets [one set contains the vertices included in MST and the other contains the fringe vertices.]
Illustration of Prim’s Algorithm:
Consider the following graph as an example for which we need to find the Minimum Spanning Tree (MST).
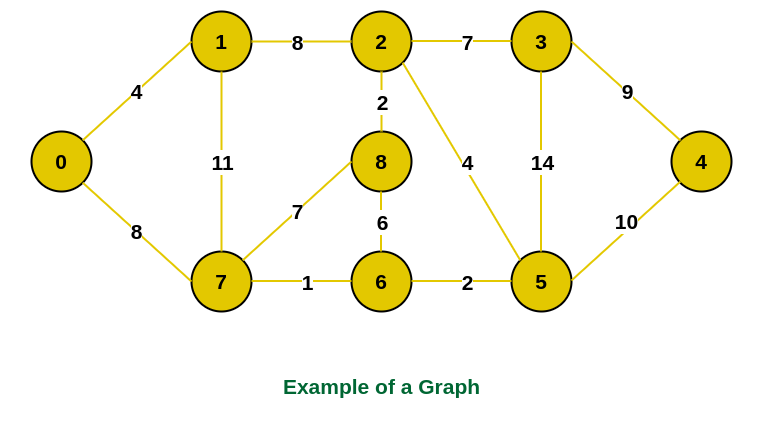
Example of a graph
Step 1: Firstly, we select an arbitrary vertex that acts as the starting vertex of the Minimum Spanning Tree. Here we have selected vertex 0 as the starting vertex.
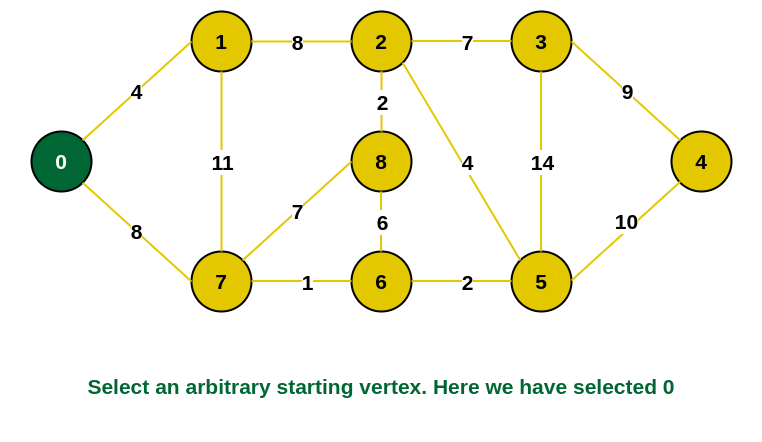
0 is selected as starting vertex
Step 2: All the edges connecting the incomplete MST and other vertices are the edges {0, 1} and {0, 7}. Between these two the edge with minimum weight is {0, 1}. So include the edge and vertex 1 in the MST.
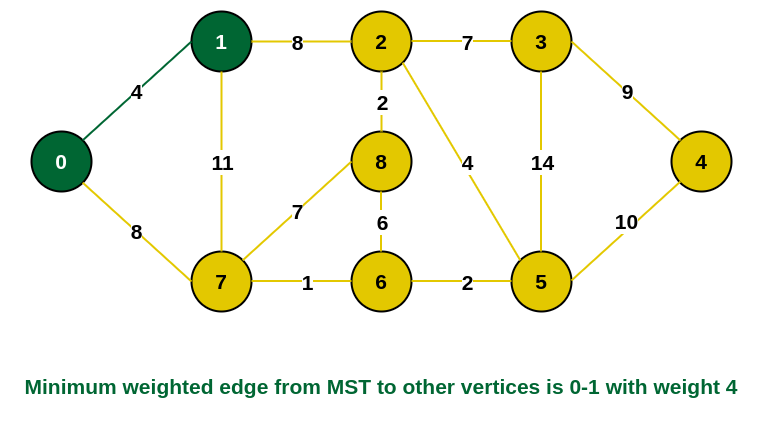
1 is added to the MST
Step 3: The edges connecting the incomplete MST to other vertices are {0, 7}, {1, 7} and {1, 2}. Among these edges the minimum weight is 8 which is of the edges {0, 7} and {1, 2}. Let us here include the edge {0, 7} and the vertex 7 in the MST. [We could have also included edge {1, 2} and vertex 2 in the MST].
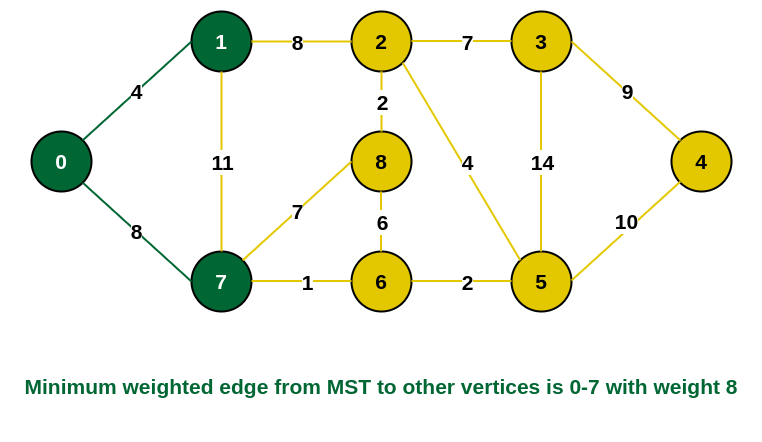
7 is added in the MST
Step 4: The edges that connect the incomplete MST with the fringe vertices are {1, 2}, {7, 6} and {7, 8}. Add the edge {7, 6} and the vertex 6 in the MST as it has the least weight (i.e., 1).
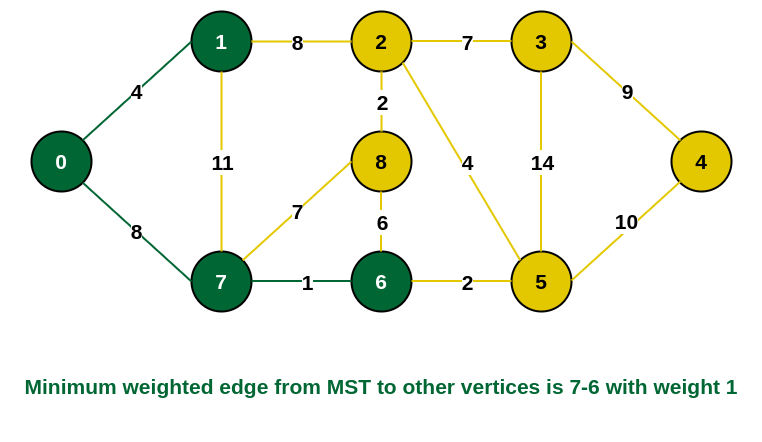
6 is added in the MST
Step 5: The connecting edges now are {7, 8}, {1, 2}, {6, 8} and {6, 5}. Include edge {6, 5} and vertex 5 in the MST as the edge has the minimum weight (i.e., 2) among them.
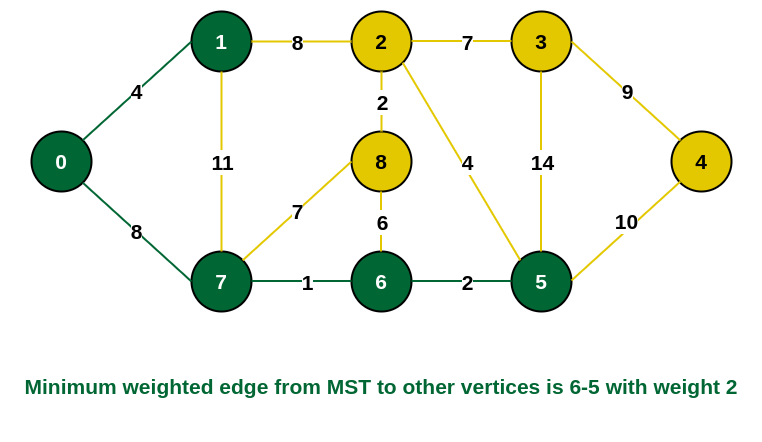
Include vertex 5 in the MST
Step 6: Among the current connecting edges, the edge {5, 2} has the minimum weight. So include that edge and the vertex 2 in the MST.
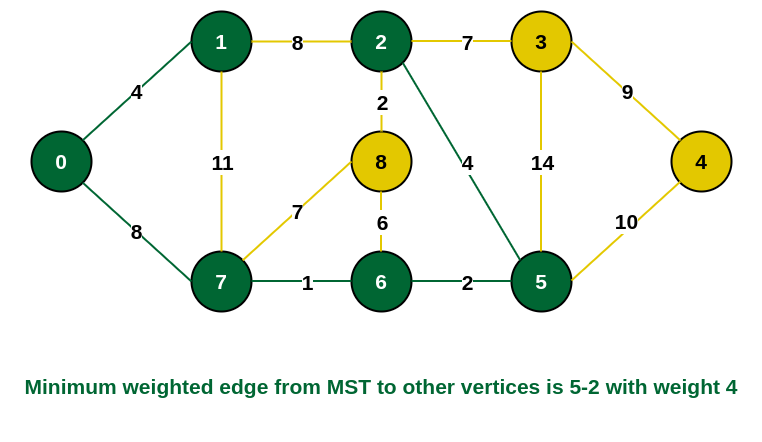
Include vertex 2 in the MST
Step 7: The connecting edges between the incomplete MST and the other edges are {2, 8}, {2, 3}, {5, 3} and {5, 4}. The edge with minimum weight is edge {2, 8} which has weight 2. So include this edge and the vertex 8 in the MST.
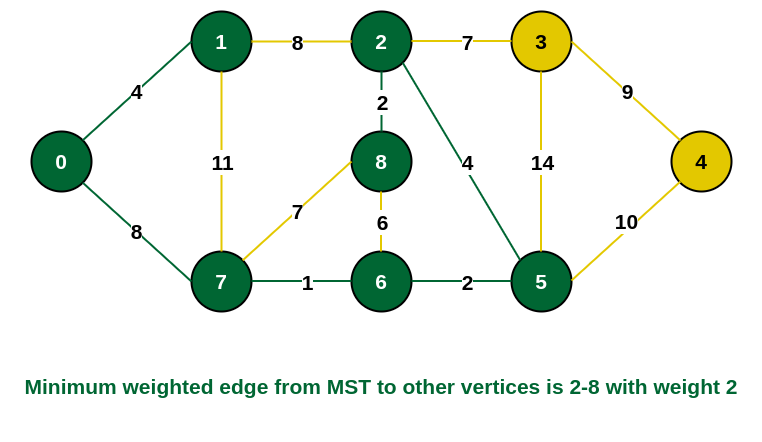
Add vertex 8 in the MST
Step 8: See here that the edges {7, 8} and {2, 3} both have same weight which are minimum. But 7 is already part of MST. So we will consider the edge {2, 3} and include that edge and vertex 3 in the MST.
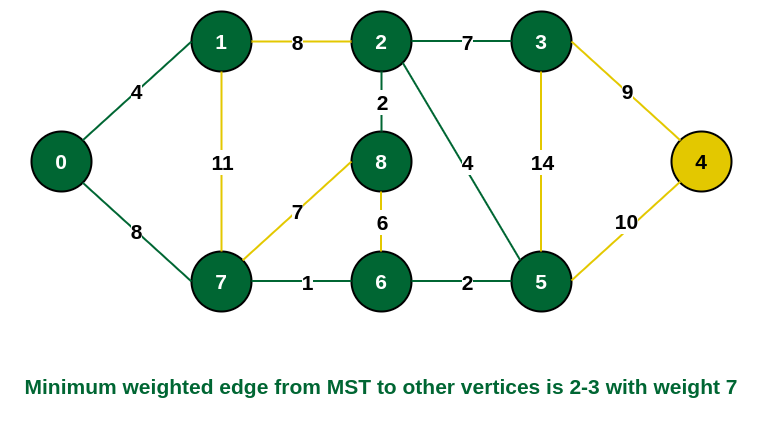
Include vertex 3 in MST
Step 9: Only the vertex 4 remains to be included. The minimum weighted edge from the incomplete MST to 4 is {3, 4}.
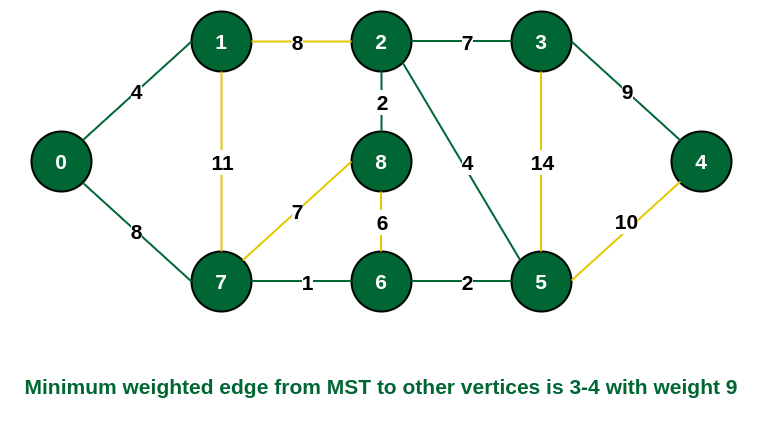
Include vertex 4 in the MST
The final structure of the MST is as follows and the weight of the edges of the MST is (4 + 8 + 1 + 2 + 4 + 2 + 7 + 9) = 37.
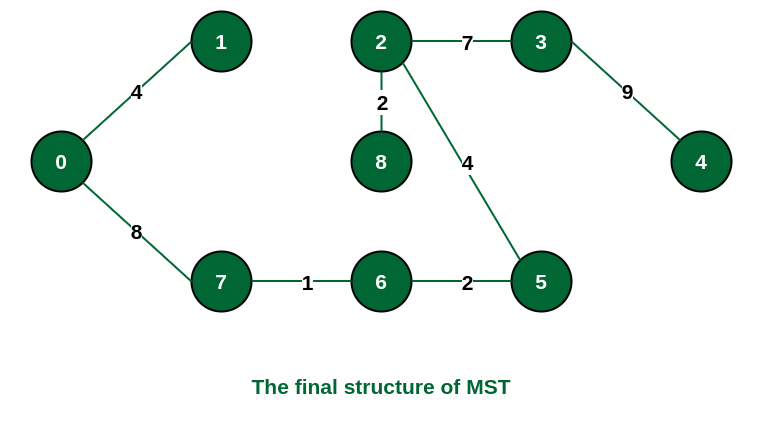
The structure of the MST formed using the above method
Note: If we had selected the edge {1, 2} in the third step then the MST would look like the following.
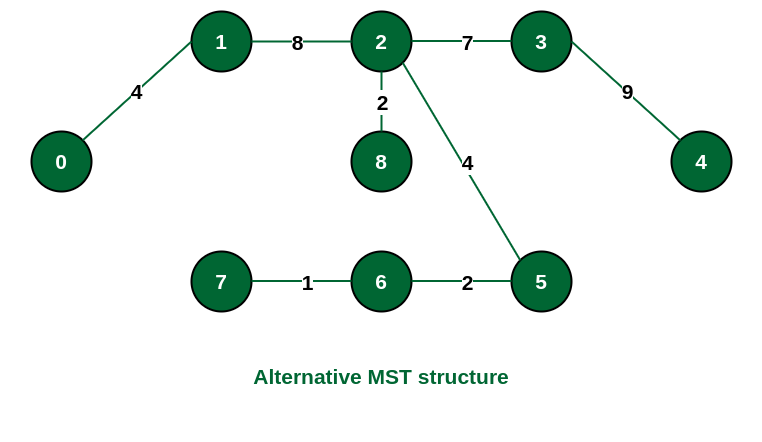
Structure of the alternate MST if we had selected edge {1, 2} in the MST
How to implement Prim’s Algorithm?
Follow the given steps to utilize the Prim’s Algorithm mentioned above for finding MST of a graph:
- Create a set mstSet that keeps track of vertices already included in MST.
- Assign a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign the key value as 0 for the first vertex so that it is picked first.
- While mstSet doesn’t include all vertices
- Pick a vertex u that is not there in mstSet and has a minimum key value.
- Include u in the mstSet.
- Update the key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices.
- For every adjacent vertex v, if the weight of edge u-v is less than the previous key value of v, update the key value as the weight of u-v.
The idea of using key values is to pick the minimum weight edge from the cut. The key values are used only for vertices that are not yet included in MST, the key value for these vertices indicates the minimum weight edges connecting them to the set of vertices included in MST.
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define V 5
int minKey(int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
void printMST(int parent[], int graph[V][V])
{
cout << "Edge \tWeight\n";
for (int i = 1; i < V; i++)
cout << parent[i] << " - " << i << " \t"
<< graph[i][parent[i]] << " \n";
}
void primMST(int graph[V][V])
{
int parent[V];
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
return 0;
}
|
C
#include <limits.h>
#include <stdbool.h>
#include <stdio.h>
#define V 5
int minKey(int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
int printMST(int parent[], int graph[V][V])
{
printf("Edge \tWeight\n");
for (int i = 1; i < V; i++)
printf("%d - %d \t%d \n", parent[i], i,
graph[i][parent[i]]);
}
void primMST(int graph[V][V])
{
int parent[V];
int key[V];
bool mstSet[V];
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class MST {
private static final int V = 5;
int minKey(int key[], Boolean mstSet[])
{
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
void printMST(int parent[], int graph[][])
{
System.out.println("Edge \tWeight");
for (int i = 1; i < V; i++)
System.out.println(parent[i] + " - " + i + "\t"
+ graph[i][parent[i]]);
}
void primMST(int graph[][])
{
int parent[] = new int[V];
int key[] = new int[V];
Boolean mstSet[] = new Boolean[V];
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u][v] != 0 && mstSet[v] == false
&& graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
printMST(parent, graph);
}
public static void main(String[] args)
{
MST t = new MST();
int graph[][] = new int[][] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
t.primMST(graph);
}
}
|
Python3
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printMST(self, parent):
print("Edge \tWeight")
for i in range(1, self.V):
print(parent[i], "-", i, "\t", self.graph[i][parent[i]])
def minKey(self, key, mstSet):
min = sys.maxsize
for v in range(self.V):
if key[v] < min and mstSet[v] == False:
min = key[v]
min_index = v
return min_index
def primMST(self):
key = [sys.maxsize] * self.V
parent = [None] * self.V
key[0] = 0
mstSet = [False] * self.V
parent[0] = -1
for cout in range(self.V):
u = self.minKey(key, mstSet)
mstSet[u] = True
for v in range(self.V):
if self.graph[u][v] > 0 and mstSet[v] == False \
and key[v] > self.graph[u][v]:
key[v] = self.graph[u][v]
parent[v] = u
self.printMST(parent)
if __name__ == '__main__':
g = Graph(5)
g.graph = [[0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]]
g.primMST()
|
C#
using System;
class MST {
static int V = 5;
static int minKey(int[] key, bool[] mstSet)
{
int min = int.MaxValue, min_index = -1;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
static void printMST(int[] parent, int[, ] graph)
{
Console.WriteLine("Edge \tWeight");
for (int i = 1; i < V; i++)
Console.WriteLine(parent[i] + " - " + i + "\t"
+ graph[i, parent[i]]);
}
static void primMST(int[, ] graph)
{
int[] parent = new int[V];
int[] key = new int[V];
bool[] mstSet = new bool[V];
for (int i = 0; i < V; i++) {
key[i] = int.MaxValue;
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u, v] != 0 && mstSet[v] == false
&& graph[u, v] < key[v]) {
parent[v] = u;
key[v] = graph[u, v];
}
}
printMST(parent, graph);
}
public static void Main()
{
int[, ] graph = new int[, ] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
primMST(graph);
}
}
|
Javascript
<script>
let V = 5;
function minKey(key, mstSet)
{
let min = Number.MAX_VALUE, min_index;
for (let v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
function printMST(parent, graph)
{
document.write("Edge Weight" + "<br>");
for (let i = 1; i < V; i++)
document.write(parent[i] + " - " + i + " " + graph[i][parent[i]] + "<br>");
}
function primMST(graph)
{
let parent = [];
let key = [];
let mstSet = [];
for (let i = 0; i < V; i++)
key[i] = Number.MAX_VALUE, mstSet[i] = false;
key[0] = 0;
parent[0] = -1;
for (let count = 0; count < V - 1; count++)
{
let u = minKey(key, mstSet);
mstSet[u] = true;
for (let v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
printMST(parent, graph);
}
let graph = [ [ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ] ];
primMST(graph);
</script>
|
Output
Edge Weight
0 - 1 2
1 - 2 3
0 - 3 6
1 - 4 5
Complexity Analysis of Prim’s Algorithm:
Time Complexity: O(V2), If the input graph is represented using an adjacency list, then the time complexity of Prim’s algorithm can be reduced to O(E * logV) with the help of a binary heap. In this implementation, we are always considering the spanning tree to start from the root of the graph
Auxiliary Space: O(V)
Other Implementations of Prim’s Algorithm:
Given below are some other implementations of Prim’s Algorithm
OPTIMIZED APPROACH OF PRIM’S ALGORITHM:
Intuition
- We transform the adjacency matrix into adjacency list using ArrayList<ArrayList<Integer>>.
- Then we create a Pair class to store the vertex and its weight .
- We sort the list on the basis of lowest weight.
- We create priority queue and push the first vertex and its weight in the queue
- Then we just traverse through its edges and store the least weight in a variable called ans.
- At last after all the vertex we return the ans.
Implementation
C++
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
int spanningTree(int V, int E, int edges[][3])
{
vector<vector<int>> adj[V];
for (int i = 0; i < E; i++) {
int u = edges[i][0];
int v = edges[i][1];
int wt = edges[i][2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
priority_queue<pii, vector<pii>, greater<pii>> pq;
vector<bool> visited(V, false);
int res = 0;
pq.push({0, 0});
while(!pq.empty()){
auto p = pq.top();
pq.pop();
int wt = p.first;
int u = p.second;
if(visited[u] == true){
continue;
}
res += wt;
visited[u] = true;
for(auto v : adj[u]){
if(visited[v[0]] == false){
pq.push({v[1], v[0]});
}
}
}
return res;
}
int main()
{
int graph[][3] = {{0, 1, 5},
{1, 2, 3},
{0, 2, 1}};
cout << spanningTree(3, 3, graph) << endl;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class Pair implements Comparable<Pair>
{
int v;
int wt;
Pair(int v,int wt)
{
this.v=v;
this.wt=wt;
}
public int compareTo(Pair that)
{
return this.wt-that.wt;
}
}
class GFG {
static int spanningTree(int V, int E, int edges[][])
{
ArrayList<ArrayList<Pair>> adj=new ArrayList<>();
for(int i=0;i<V;i++)
{
adj.add(new ArrayList<Pair>());
}
for(int i=0;i<edges.length;i++)
{
int u=edges[i][0];
int v=edges[i][1];
int wt=edges[i][2];
adj.get(u).add(new Pair(v,wt));
adj.get(v).add(new Pair(u,wt));
}
PriorityQueue<Pair> pq = new PriorityQueue<Pair>();
pq.add(new Pair(0,0));
int[] vis=new int[V];
int s=0;
while(!pq.isEmpty())
{
Pair node=pq.poll();
int v=node.v;
int wt=node.wt;
if(vis[v]==1)
continue;
s+=wt;
vis[v]=1;
for(Pair it:adj.get(v))
{
if(vis[it.v]==0)
{
pq.add(new Pair(it.v,it.wt));
}
}
}
return s;
}
public static void main (String[] args) {
int graph[][] = new int[][] {{0,1,5},
{1,2,3},
{0,2,1}};
System.out.println(spanningTree(3,3,graph));
}
}
|
Python3
import heapq
def tree(V, E, edges):
adj = [[] for _ in range(V)]
for i in range(E):
u, v, wt = edges[i]
adj[u].append((v, wt))
adj[v].append((u, wt))
pq = []
visited = [False] * V
res = 0
heapq.heappush(pq, (0, 0))
while pq:
wt, u = heapq.heappop(pq)
if visited[u]:
continue
res += wt
visited[u] = True
for v, weight in adj[u]:
if not visited[v]:
heapq.heappush(pq, (weight, v))
return res
if __name__ == "__main__":
graph = [[0, 1, 5],
[1, 2, 3],
[0, 2, 1]]
print(tree(3, 3, graph))
|
C#
using System;
using System.Collections.Generic;
public class MinimumSpanningTree
{
public static int SpanningTree(int V, int E, int[,] edges)
{
List<List<int[]>> adj = new List<List<int[]>>();
for (int i = 0; i < V; i++)
{
adj.Add(new List<int[]>());
}
for (int i = 0; i < E; i++)
{
int u = edges[i, 0];
int v = edges[i, 1];
int wt = edges[i, 2];
adj[u].Add(new int[] { v, wt });
adj[v].Add(new int[] { u, wt });
}
PriorityQueue<(int, int)> pq = new PriorityQueue<(int, int)>();
bool[] visited = new bool[V];
int res = 0;
pq.Enqueue((0, 0));
while (pq.Count > 0)
{
var p = pq.Dequeue();
int wt = p.Item1;
int u = p.Item2;
if (visited[u])
{
continue;
}
res += wt;
visited[u] = true;
foreach (var v in adj[u])
{
if (!visited[v[0]])
{
pq.Enqueue((v[1], v[0]));
}
}
}
return res;
}
public static void Main()
{
int[,] graph = { { 0, 1, 5 }, { 1, 2, 3 }, { 0, 2, 1 } };
Console.WriteLine(SpanningTree(3, 3, graph));
}
}
public class PriorityQueue<T> where T : IComparable<T>
{
private List<T> heap = new List<T>();
public int Count => heap.Count;
public void Enqueue(T item)
{
heap.Add(item);
int i = heap.Count - 1;
while (i > 0)
{
int parent = (i - 1) / 2;
if (heap[parent].CompareTo(heap[i]) <= 0)
break;
Swap(parent, i);
i = parent;
}
}
public T Dequeue()
{
int lastIndex = heap.Count - 1;
T frontItem = heap[0];
heap[0] = heap[lastIndex];
heap.RemoveAt(lastIndex);
--lastIndex;
int parent = 0;
while (true)
{
int leftChild = parent * 2 + 1;
if (leftChild > lastIndex)
break;
int rightChild = leftChild + 1;
if (rightChild <= lastIndex && heap[leftChild].CompareTo(heap[rightChild]) > 0)
leftChild = rightChild;
if (heap[parent].CompareTo(heap[leftChild]) <= 0)
break;
Swap(parent, leftChild);
parent = leftChild;
}
return frontItem;
}
private void Swap(int i, int j)
{
T temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
}
|
Javascript
class PriorityQueue {
constructor() {
this.heap = [];
}
enqueue(value) {
this.heap.push(value);
let i = this.heap.length - 1;
while (i > 0) {
let j = Math.floor((i - 1) / 2);
if (this.heap[i][0] >= this.heap[j][0]) {
break;
}
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
i = j;
}
}
dequeue() {
if (this.heap.length === 0) {
throw new Error("Queue is empty");
}
let i = this.heap.length - 1;
const result = this.heap[0];
this.heap[0] = this.heap[i];
this.heap.pop();
i--;
let j = 0;
while (true) {
const left = j * 2 + 1;
if (left > i) {
break;
}
const right = left + 1;
let k = left;
if (right <= i && this.heap[right][0] < this.heap[left][0]) {
k = right;
}
if (this.heap[j][0] <= this.heap[k][0]) {
break;
}
[this.heap[j], this.heap[k]] = [this.heap[k], this.heap[j]];
j = k;
}
return result;
}
get count() {
return this.heap.length;
}
}
function spanningTree(V, E, edges) {
const adj = new Array(V).fill(null).map(() => []);
for (let i = 0; i < E; i++) {
const [u, v, wt] = edges[i];
adj[u].push([v, wt]);
adj[v].push([u, wt]);
}
const pq = new PriorityQueue();
const visited = new Array(V).fill(false);
let res = 0;
pq.enqueue([0, 0]);
while (pq.count > 0) {
const p = pq.dequeue();
const wt = p[0];
const u = p[1];
if (visited[u]) {
continue;
}
res += wt;
visited[u] = true;
for (const v of adj[u]) {
if (!visited[v[0]]) {
pq.enqueue([v[1], v[0]]);
}
}
}
return res;
}
const graph = [[0, 1, 5], [1, 2, 3], [0, 2, 1]];
console.log(spanningTree(3, 3, graph));
|
Complexity Analysis of Prim’s Algorithm:
Time Complexity: O(E*log(E)) where E is the number of edges
Auxiliary Space: O(V^2) where V is the number of vertex
Prim’s algorithm for finding the minimum spanning tree (MST):
Advantages:
- Prim’s algorithm is guaranteed to find the MST in a connected, weighted graph.
- It has a time complexity of O(E log V) using a binary heap or Fibonacci heap, where E is the number of edges and V is the number of vertices.
- It is a relatively simple algorithm to understand and implement compared to some other MST algorithms.
Disadvantages:
- Like Kruskal’s algorithm, Prim’s algorithm can be slow on dense graphs with many edges, as it requires iterating over all edges at least once.
- Prim’s algorithm relies on a priority queue, which can take up extra memory and slow down the algorithm on very large graphs.
- The choice of starting node can affect the MST output, which may not be desirable in some applications.
Please Login to comment...