Introduction to Binary Tree – Data Structure and Algorithm Tutorials
Last Updated :
19 Jun, 2024
Binary Tree is a non-linear data structure where each node has at most two children. In this article, we will cover all the basics of Binary Tree, Operations on Binary Tree, its implementation, advantages, disadvantages which will help you solve all the problems based on Binary Tree.
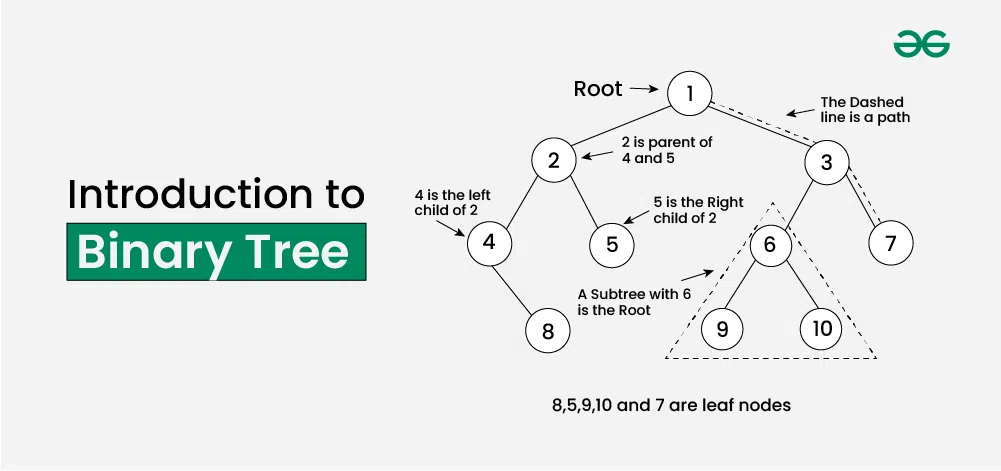
What is Binary Tree?
Binary tree is a tree data structure(non-linear) in which each node can have at most two children which are referred to as the left child and the right child.
The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. A binary tree can be visualized as a hierarchical structure with the root at the top and the leaves at the bottom.
Representation of Binary Tree
Each node in a Binary Tree has three parts:
- Data
- Pointer to the left child
- Pointer to the right child
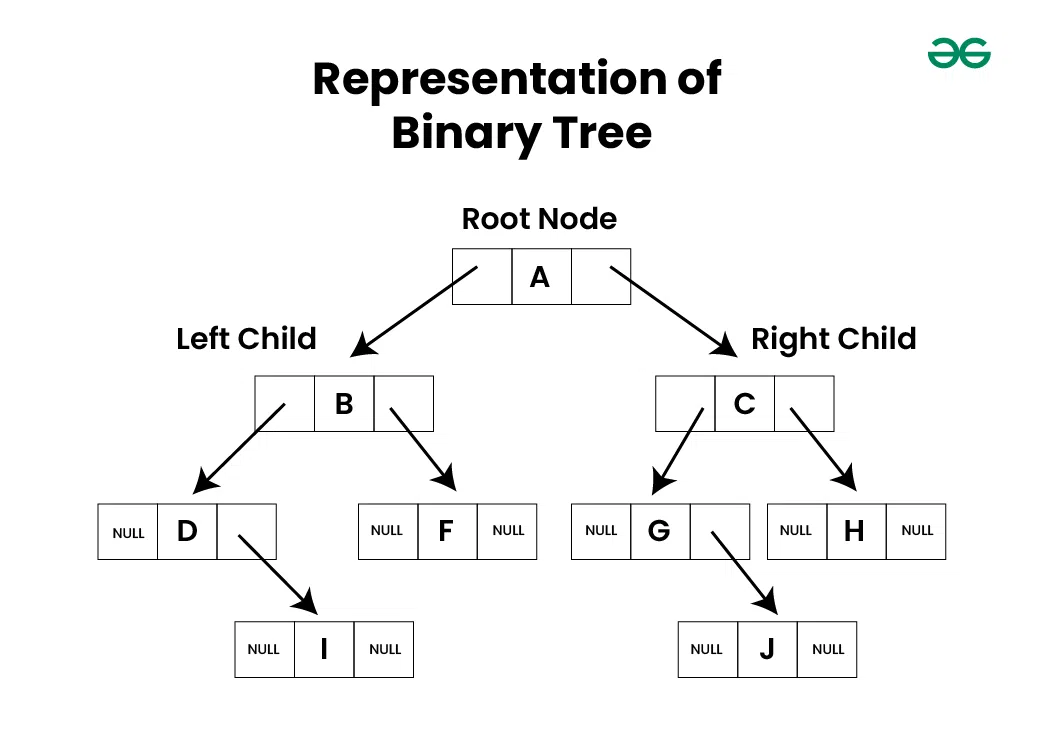
Below is the representation of a Node of Binary Tree in different languages:
C++
// Use any below method to implement Nodes of tree
// Method 1: Using "struct" to make
// user-define data type
struct node {
int data;
struct node* left;
struct node* right;
};
// Method 2: Using "class" to make
// user-define data type
class Node {
public:
int data;
Node* left;
Node* right;
};
// Structure of each node of the tree
struct node {
int data;
struct node* left;
struct node* right;
};
// Class containing left and right child
// of current node and key value
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
# A Python class that represents
# an individual node in a Binary Tree
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
// Class containing left and right child
// of current node and key value
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
<script>
/* Class containing left and right child of current
node and key value*/
class Node
{
constructor(item)
{
this.key = item;
this.left = this.right = null;
}
}
// This code is contributed by umadevi9616
</script>
Types of Binary Tree
Binary Tree can be classified into multiples types based on multiple factors:
- On the basis of Number of Children
- On the basis of Completion of Levels
- On the basis of Node Values:
Operations On Binary Tree
1. Insertion in Binary Tree
We can insert a node anywhere in a binary tree by inserting the node as the left or right child of any node or by making the node as root of the tree.
Algorithm to insert a node in a Binary Tree:
- Check if there is a node in the binary tree, which has missing left child. If such a node exists, then insert the new node as its left child.
- Check if there is a node in the binary tree, which has missing right child. If such a node exists, then insert the new node as its right child.
- If we don’t find any node with missing left or right child, then find the node which has both the children missing and insert the node as its left or right child.
2. Traversal of Binary Tree
Traversal of Binary Tree involves visiting all the nodes of the binary tree. Tree Traversal algorithms can be classified broadly into two categories:
- Depth-First Search (DFS) Algorithms
- Breadth-First Search (BFS) Algorithms
Depth-First Search (DFS) algorithms:
- Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.
- Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It means that the left child is traversed first then its root node and finally the right child.
- Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first then the right child and finally its root node.
Breadth-First Search (BFS) algorithms:
- Level Order Traversal: Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.
3. Deletion in Binary Tree
We can delete any node in the binary tree and rearrange the nodes after deletion to again form a valid binary tree.
Algorithm to delete a node in a Binary Tree:
- Starting at the root, find the deepest and rightmost node in the binary tree and the node which we want to delete.
- Replace the deepest rightmost node’s data with the node to be deleted.
- Then delete the deepest rightmost node.
4. Searching in Binary Tree
We can search for an element in the node by using any of the traversal techniques.
Algorithm to search a node in a Binary Tree:
- Start from the root node.
- Check if the current node’s value is equal to the target value.
- If the current node’s value is equal to the target value, then this node is the required node.
- Otherwise, if the node’s value is not equal to the target value, start the search in the left and right child.
- If we do not find any node whose value is equal to target, then the value is not present in the tree.
Auxiliary Operations On Binary Tree
Implementation of Binary Tree
Below is the code for insertion, deletion and traversal of the binary tree:
C++14
#include <bits/stdc++.h>
using namespace std;
// Node class to define the structure of the node
class Node {
public:
int data;
Node *left, *right;
// Parameterized Constructor
Node(int val)
{
data = val;
left = right = NULL;
}
};
// Function to insert nodes
Node* insert(Node* root, int data)
{
// If tree is empty, new node becomes the root
if (root == NULL) {
root = new Node(data);
return root;
}
// queue to traverse the tree and find the position to
// insert the node
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* temp = q.front();
q.pop();
// Insert node as the left child of the parent node
if (temp->left == NULL) {
temp->left = new Node(data);
break;
}
// If the left child is not null push it to the
// queue
else
q.push(temp->left);
// Insert node as the right child of parent node
if (temp->right == NULL) {
temp->right = new Node(data);
break;
}
// If the right child is not null push it to the
// queue
else
q.push(temp->right);
}
return root;
}
/* function to delete the given deepest node
(d_node) in binary tree */
void deletDeepest(Node* root, Node* d_node)
{
queue<Node*> q;
q.push(root);
// Do level order traversal until last node
Node* temp;
while (!q.empty()) {
temp = q.front();
q.pop();
if (temp == d_node) {
temp = NULL;
delete (d_node);
return;
}
if (temp->right) {
if (temp->right == d_node) {
temp->right = NULL;
delete (d_node);
return;
}
else
q.push(temp->right);
}
if (temp->left) {
if (temp->left == d_node) {
temp->left = NULL;
delete (d_node);
return;
}
else
q.push(temp->left);
}
}
}
/* function to delete element in binary tree */
Node* deletion(Node* root, int key)
{
if (!root)
return NULL;
if (root->left == NULL && root->right == NULL) {
if (root->data == key)
return NULL;
else
return root;
}
queue<Node*> q;
q.push(root);
Node* temp;
Node* key_node = NULL;
// Do level order traversal to find deepest
// node(temp) and node to be deleted (key_node)
while (!q.empty()) {
temp = q.front();
q.pop();
if (temp->data == key)
key_node = temp;
if (temp->left)
q.push(temp->left);
if (temp->right)
q.push(temp->right);
}
if (key_node != NULL) {
int x = temp->data;
key_node->data = x;
deletDeepest(root, temp);
}
return root;
}
// Inorder tree traversal (Left - Root - Right)
void inorderTraversal(Node* root)
{
if (!root)
return;
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
// Preorder tree traversal (Root - Left - Right)
void preorderTraversal(Node* root)
{
if (!root)
return;
cout << root->data << " ";
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// Postorder tree traversal (Left - Right - Root)
void postorderTraversal(Node* root)
{
if (root == NULL)
return;
postorderTraversal(root->left);
postorderTraversal(root->right);
cout << root->data << " ";
}
// Function for Level order tree traversal
void levelorderTraversal(Node* root)
{
if (root == NULL)
return;
// Queue for level order traversal
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* temp = q.front();
q.pop();
cout << temp->data << " ";
// Push left child in the queue
if (temp->left)
q.push(temp->left);
// Push right child in the queue
if (temp->right)
q.push(temp->right);
}
}
/* Driver function to check the above algorithm. */
int main()
{
Node* root = NULL;
// Insertion of nodes
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
cout << "Preorder traversal: ";
preorderTraversal(root);
cout << "\nInorder traversal: ";
inorderTraversal(root);
cout << "\nPostorder traversal: ";
postorderTraversal(root);
cout << "\nLevel order traversal: ";
levelorderTraversal(root);
// Delete the node with data = 20
root = deletion(root, 20);
cout << "\nInorder traversal after deletion: ";
inorderTraversal(root);
}
#include <stdio.h>
// Node structure to define the structure of the node
typedef struct Node {
int data;
struct Node *left, *right;
} Node;
// Function to create a new node
Node* newNode(int val) {
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = val;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert nodes
Node* insert(Node* root, int data) {
// If tree is empty, new node becomes the root
if (root == NULL) {
root = newNode(data);
return root;
}
// Queue to traverse the tree and find the position to insert the node
Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
while (front != rear) {
Node* temp = queue[front++];
// Insert node as the left child of the parent node
if (temp->left == NULL) {
temp->left = newNode(data);
break;
}
// If the left child is not null, push it to the queue
else
queue[rear++] = temp->left;
// Insert node as the right child of parent node
if (temp->right == NULL) {
temp->right = newNode(data);
break;
}
// If the right child is not null, push it to the queue
else
queue[rear++] = temp->right;
}
return root;
}
/* Function to delete the given deepest node (d_node) in binary tree */
void deletDeepest(Node* root, Node* d_node) {
Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
// Do level order traversal until last node
Node* temp;
while (front != rear) {
temp = queue[front++];
if (temp == d_node) {
temp = NULL;
free(d_node);
return;
}
if (temp->right) {
if (temp->right == d_node) {
temp->right = NULL;
free(d_node);
return;
} else
queue[rear++] = temp->right;
}
if (temp->left) {
if (temp->left == d_node) {
temp->left = NULL;
free(d_node);
return;
} else
queue[rear++] = temp->left;
}
}
}
/* Function to delete element in binary tree */
Node* deletion(Node* root, int key) {
if (!root)
return NULL;
if (root->left == NULL && root->right == NULL) {
if (root->data == key)
return NULL;
else
return root;
}
Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
Node* temp;
Node* key_node = NULL;
// Do level order traversal to find deepest node (temp) and node to be deleted (key_node)
while (front != rear) {
temp = queue[front++];
if (temp->data == key)
key_node = temp;
if (temp->left)
queue[rear++] = temp->left;
if (temp->right)
queue[rear++] = temp->right;
}
if (key_node != NULL) {
int x = temp->data;
key_node->data = x;
deletDeepest(root, temp);
}
return root;
}
// Inorder tree traversal (Left - Root - Right)
void inorderTraversal(Node* root) {
if (!root)
return;
inorderTraversal(root->left);
printf("%d ", root->data);
inorderTraversal(root->right);
}
// Preorder tree traversal (Root - Left - Right)
void preorderTraversal(Node* root) {
if (!root)
return;
printf("%d ", root->data);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// Postorder tree traversal (Left - Right - Root)
void postorderTraversal(Node* root) {
if (root == NULL)
return;
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%d ", root->data);
}
// Function for Level order tree traversal
void levelorderTraversal(Node* root) {
if (root == NULL)
return;
// Queue for level order traversal
Node* queue[100];
int front = 0, rear = 0;
queue[rear++] = root;
while (front != rear) {
Node* temp = queue[front++];
printf("%d ", temp->data);
// Push left child in the queue
if (temp->left)
queue[rear++] = temp->left;
// Push right child in the queue
if (temp->right)
queue[rear++] = temp->right;
}
}
/* Driver function to check the above algorithm. */
int main() {
Node* root = NULL;
// Insertion of nodes
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
printf("Preorder traversal: ");
preorderTraversal(root);
printf("\nInorder traversal: ");
inorderTraversal(root);
printf("\nPostorder traversal: ");
postorderTraversal(root);
printf("\nLevel order traversal: ");
levelorderTraversal(root);
// Delete the node with data = 20
root = deletion(root, 20);
printf("\nInorder traversal after deletion: ");
inorderTraversal(root);
return 0;
}
import java.util.LinkedList;
import java.util.Queue;
// Node class to define the structure of the node
class Node {
int data;
Node left, right;
// Parameterized Constructor
Node(int val) {
data = val;
left = right = null;
}
}
public class BinaryTree {
// Function to insert nodes
public static Node insert(Node root, int data) {
// If tree is empty, new node becomes the root
if (root == null) {
root = new Node(data);
return root;
}
// Queue to traverse the tree and find the position to
// insert the node
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
Node temp = q.poll();
// Insert node as the left child of the parent node
if (temp.left == null) {
temp.left = new Node(data);
break;
}
// If the left child is not null push it to the
// queue
else
q.offer(temp.left);
// Insert node as the right child of parent node
if (temp.right == null) {
temp.right = new Node(data);
break;
}
// If the right child is not null push it to the
// queue
else
q.offer(temp.right);
}
return root;
}
/* function to delete the given deepest node
(d_node) in binary tree */
public static void deletDeepest(Node root, Node d_node) {
Queue<Node> q = new LinkedList<>();
q.offer(root);
// Do level order traversal until last node
Node temp;
while (!q.isEmpty()) {
temp = q.poll();
if (temp == d_node) {
temp = null;
d_node = null;
return;
}
if (temp.right != null) {
if (temp.right == d_node) {
temp.right = null;
d_node = null;
return;
} else
q.offer(temp.right);
}
if (temp.left != null) {
if (temp.left == d_node) {
temp.left = null;
d_node = null;
return;
} else
q.offer(temp.left);
}
}
}
/* function to delete element in binary tree */
public static Node deletion(Node root, int key) {
if (root == null)
return null;
if (root.left == null && root.right == null) {
if (root.data == key)
return null;
else
return root;
}
Queue<Node> q = new LinkedList<>();
q.offer(root);
Node temp = new Node(0);
Node key_node = null;
// Do level order traversal to find deepest
// node(temp) and node to be deleted (key_node)
while (!q.isEmpty()) {
temp = q.poll();
if (temp.data == key)
key_node = temp;
if (temp.left != null)
q.offer(temp.left);
if (temp.right != null)
q.offer(temp.right);
}
if (key_node != null) {
int x = temp.data;
key_node.data = x;
deletDeepest(root, temp);
}
return root;
}
// Inorder tree traversal (Left - Root - Right)
public static void inorderTraversal(Node root) {
if (root == null)
return;
inorderTraversal(root.left);
System.out.print(root.data + " ");
inorderTraversal(root.right);
}
// Preorder tree traversal (Root - Left - Right)
public static void preorderTraversal(Node root) {
if (root == null)
return;
System.out.print(root.data + " ");
preorderTraversal(root.left);
preorderTraversal(root.right);
}
// Postorder tree traversal (Left - Right - Root)
public static void postorderTraversal(Node root) {
if (root == null)
return;
postorderTraversal(root.left);
postorderTraversal(root.right);
System.out.print(root.data + " ");
}
// Function for Level order tree traversal
public static void levelorderTraversal(Node root) {
if (root == null)
return;
// Queue for level order traversal
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
Node temp = q.poll();
System.out.print(temp.data + " ");
// Push left child in the queue
if (temp.left != null)
q.offer(temp.left);
// Push right child in the queue
if (temp.right != null)
q.offer(temp.right);
}
}
/* Driver function to check the above algorithm. */
public static void main(String[] args) {
Node root = null;
// Insertion of nodes
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
System.out.print("Preorder traversal: ");
preorderTraversal(root);
System.out.print("\nInorder traversal: ");
inorderTraversal(root);
System.out.print("\nPostorder traversal: ");
postorderTraversal(root);
System.out.print("\nLevel order traversal: ");
levelorderTraversal(root);
// Delete the node with data = 20
root = deletion(root, 20);
System.out.print("\nInorder traversal after deletion: ");
inorderTraversal(root);
}
}
from collections import deque
# Node class to define the structure of the node
class Node:
def __init__(self, val):
self.data = val
self.left = self.right = None
# Function to insert nodes
def insert(root, data):
# If tree is empty, new node becomes the root
if root is None:
root = Node(data)
return root
# Queue to traverse the tree and find the position to insert the node
q = deque()
q.append(root)
while q:
temp = q.popleft()
# Insert node as the left child of the parent node
if temp.left is None:
temp.left = Node(data)
break
# If the left child is not null push it to the queue
else:
q.append(temp.left)
# Insert node as the right child of parent node
if temp.right is None:
temp.right = Node(data)
break
# If the right child is not null push it to the queue
else:
q.append(temp.right)
return root
# Function to delete the given deepest node (d_node) in binary tree
def deletDeepest(root, d_node):
q = deque()
q.append(root)
# Do level order traversal until last node
while q:
temp = q.popleft()
if temp == d_node:
temp = None
del d_node
return
if temp.right:
if temp.right == d_node:
temp.right = None
del d_node
return
else:
q.append(temp.right)
if temp.left:
if temp.left == d_node:
temp.left = None
del d_node
return
else:
q.append(temp.left)
# Function to delete element in binary tree
def deletion(root, key):
if not root:
return None
if root.left is None and root.right is None:
if root.data == key:
return None
else:
return root
q = deque()
q.append(root)
temp = None
key_node = None
# Do level order traversal to find deepest node (temp) and node to be deleted (key_node)
while q:
temp = q.popleft()
if temp.data == key:
key_node = temp
if temp.left:
q.append(temp.left)
if temp.right:
q.append(temp.right)
if key_node is not None:
x = temp.data
key_node.data = x
deletDeepest(root, temp)
return root
# Inorder tree traversal (Left - Root - Right)
def inorderTraversal(root):
if not root:
return
inorderTraversal(root.left)
print(root.data, end=" ")
inorderTraversal(root.right)
# Preorder tree traversal (Root - Left - Right)
def preorderTraversal(root):
if not root:
return
print(root.data, end=" ")
preorderTraversal(root.left)
preorderTraversal(root.right)
# Postorder tree traversal (Left - Right - Root)
def postorderTraversal(root):
if root is None:
return
postorderTraversal(root.left)
postorderTraversal(root.right)
print(root.data, end=" ")
# Function for Level order tree traversal
def levelorderTraversal(root):
if root is None:
return
# Queue for level order traversal
q = deque()
q.append(root)
while q:
temp = q.popleft()
print(temp.data, end=" ")
# Push left child in the queue
if temp.left:
q.append(temp.left)
# Push right child in the queue
if temp.right:
q.append(temp.right)
# Driver function to check the above algorithm
if __name__ == "__main__":
root = None
# Insertion of nodes
root = insert(root, 10)
root = insert(root, 20)
root = insert(root, 30)
root = insert(root, 40)
print("Preorder traversal:", end=" ")
preorderTraversal(root)
print("\nInorder traversal:", end=" ")
inorderTraversal(root)
print("\nPostorder traversal:", end=" ")
postorderTraversal(root)
print("\nLevel order traversal:", end=" ")
levelorderTraversal(root)
# Delete the node with data = 20
root = deletion(root, 20)
print("\nInorder traversal after deletion:", end=" ")
inorderTraversal(root)
using System;
using System.Collections.Generic;
// Node class to define the structure of the node
public class Node
{
public int data;
public Node left, right;
// Parameterized Constructor
public Node(int val)
{
data = val;
left = right = null;
}
}
public class Program
{
// Function to insert nodes
public static Node Insert(Node root, int data)
{
// If tree is empty, new node becomes the root
if (root == null)
{
root = new Node(data);
return root;
}
// Queue to traverse the tree and find the position to insert the node
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
while (q.Count != 0)
{
Node temp = q.Dequeue();
// Insert node as the left child of the parent node
if (temp.left == null)
{
temp.left = new Node(data);
break;
}
// If the left child is not null, push it to the queue
else
q.Enqueue(temp.left);
// Insert node as the right child of parent node
if (temp.right == null)
{
temp.right = new Node(data);
break;
}
// If the right child is not null, push it to the queue
else
q.Enqueue(temp.right);
}
return root;
}
/* function to delete the given deepest node (d_node) in binary tree */
public static void DeleteDeepest(Node root, Node d_node)
{
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
// Do level order traversal until last node
Node temp;
while (q.Count != 0)
{
temp = q.Dequeue();
if (temp == d_node)
{
temp = null;
d_node = null;
return;
}
if (temp.right != null)
{
if (temp.right == d_node)
{
temp.right = null;
d_node = null;
return;
}
else
q.Enqueue(temp.right);
}
if (temp.left != null)
{
if (temp.left == d_node)
{
temp.left = null;
d_node = null;
return;
}
else
q.Enqueue(temp.left);
}
}
}
/* function to delete element in binary tree */
public static Node Deletion(Node root, int key)
{
if (root == null)
return null;
if (root.left == null && root.right == null)
{
if (root.data == key)
return null;
else
return root;
}
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
Node temp = new Node(0);
Node key_node = null;
// Do level order traversal to find deepest node (temp) and node to be deleted (key_node)
while (q.Count != 0)
{
temp = q.Dequeue();
if (temp.data == key)
key_node = temp;
if (temp.left != null)
q.Enqueue(temp.left);
if (temp.right != null)
q.Enqueue(temp.right);
}
if (key_node != null)
{
int x = temp.data;
key_node.data = x;
DeleteDeepest(root, temp);
}
return root;
}
// Inorder tree traversal (Left - Root - Right)
public static void InorderTraversal(Node root)
{
if (root == null)
return;
InorderTraversal(root.left);
Console.Write(root.data + " ");
InorderTraversal(root.right);
}
// Preorder tree traversal (Root - Left - Right)
public static void PreorderTraversal(Node root)
{
if (root == null)
return;
Console.Write(root.data + " ");
PreorderTraversal(root.left);
PreorderTraversal(root.right);
}
// Postorder tree traversal (Left - Right - Root)
public static void PostorderTraversal(Node root)
{
if (root == null)
return;
PostorderTraversal(root.left);
PostorderTraversal(root.right);
Console.Write(root.data + " ");
}
// Function for Level order tree traversal
public static void LevelorderTraversal(Node root)
{
if (root == null)
return;
// Queue for level order traversal
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
while (q.Count != 0)
{
Node temp = q.Dequeue();
Console.Write(temp.data + " ");
// Push left child in the queue
if (temp.left != null)
q.Enqueue(temp.left);
// Push right child in the queue
if (temp.right != null)
q.Enqueue(temp.right);
}
}
/* Driver function to check the above algorithm. */
public static void Main(string[] args)
{
Node root = null;
// Insertion of nodes
root = Insert(root, 10);
root = Insert(root, 20);
root = Insert(root, 30);
root = Insert(root, 40);
Console.Write("Preorder traversal: ");
PreorderTraversal(root);
Console.Write("\nInorder traversal: ");
InorderTraversal(root);
Console.Write("\nPostorder traversal: ");
PostorderTraversal(root);
Console.Write("\nLevel order traversal: ");
LevelorderTraversal(root);
// Delete the node with data = 20
root = Deletion(root, 20);
Console.Write("\nInorder traversal after deletion: ");
InorderTraversal(root);
}
}
// Node class to define the structure of the node
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
// Function to insert nodes
function insert(root, data) {
// If tree is empty, new node becomes the root
if (root === null) {
root = new Node(data);
return root;
}
// queue to traverse the tree and find the position to
// insert the node
const q = [];
q.push(root);
while (q.length !== 0) {
const temp = q.shift();
// Insert node as the left child of the parent node
if (temp.left === null) {
temp.left = new Node(data);
break;
}
// If the left child is not null push it to the
// queue
else
q.push(temp.left);
// Insert node as the right child of parent node
if (temp.right === null) {
temp.right = new Node(data);
break;
}
// If the right child is not null push it to the
// queue
else
q.push(temp.right);
}
return root;
}
/* function to delete the given deepest node
(d_node) in binary tree */
function deletDeepest(root, d_node) {
const q = [];
q.push(root);
// Do level order traversal until last node
let temp;
while (q.length !== 0) {
temp = q.shift();
if (temp === d_node) {
temp = null;
delete d_node;
return;
}
if (temp.right) {
if (temp.right === d_node) {
temp.right = null;
delete d_node;
return;
}
else
q.push(temp.right);
}
if (temp.left) {
if (temp.left === d_node) {
temp.left = null;
delete d_node;
return;
}
else
q.push(temp.left);
}
}
}
/* function to delete element in binary tree */
function deletion(root, key) {
if (!root)
return null;
if (root.left === null && root.right === null) {
if (root.data === key)
return null;
else
return root;
}
const q = [];
q.push(root);
let temp;
let key_node = null;
// Do level order traversal to find deepest
// node(temp) and node to be deleted (key_node)
while (q.length !== 0) {
temp = q.shift();
if (temp.data === key)
key_node = temp;
if (temp.left)
q.push(temp.left);
if (temp.right)
q.push(temp.right);
}
if (key_node !== null) {
const x = temp.data;
key_node.data = x;
deletDeepest(root, temp);
}
return root;
}
// Inorder tree traversal (Left - Root - Right)
function inorderTraversal(root) {
if (!root)
return;
inorderTraversal(root.left);
console.log(root.data + " ");
inorderTraversal(root.right);
}
// Preorder tree traversal (Root - Left - Right)
function preorderTraversal(root) {
if (!root)
return;
console.log(root.data + " ");
preorderTraversal(root.left);
preorderTraversal(root.right);
}
// Postorder tree traversal (Left - Right - Root)
function postorderTraversal(root) {
if (root === null)
return;
postorderTraversal(root.left);
postorderTraversal(root.right);
console.log(root.data + " ");
}
// Function for Level order tree traversal
function levelorderTraversal(root) {
if (root === null)
return;
// Queue for level order traversal
const q = [];
q.push(root);
while (q.length !== 0) {
const temp = q.shift();
console.log(temp.data + " ");
// Push left child in the queue
if (temp.left)
q.push(temp.left);
// Push right child in the queue
if (temp.right)
q.push(temp.right);
}
}
/* Driver function to check the above algorithm. */
let root = null;
// Insertion of nodes
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
console.log("Preorder traversal: ");
preorderTraversal(root);
console.log("\nInorder traversal: ");
inorderTraversal(root);
console.log("\nPostorder traversal: ");
postorderTraversal(root);
console.log("\nLevel order traversal: ");
levelorderTraversal(root);
// Delete the node with data = 20
root = deletion(root, 20);
console.log("\nInorder traversal after deletion: ");
inorderTraversal(root);
OutputPreorder traversal: 10 20 40 30
Inorder traversal: 40 20 10 30
Postorder traversal: 40 20 30 10
Level order traversal: 10 20 30 40
Inorder traversal after deletion: 40 10 30
Complexity Analysis of Binary Tree Operations
| Operations | Time Complexity | Space Complexity
|
|---|
| Insertion | O(N) | O(N)
|
|---|
| Preorder Traversal | O(N) | O(N)
|
|---|
Inorder Traversal
| O(N)
| O(N)
|
|---|
| Postorder Traversal | O(N) | O(N)
|
|---|
| Level Order Traversal | O(N) | O(N)
|
|---|
Deletion
| O(N)
| O(N)
|
|---|
Searching
| O(N)
| O(N)
|
|---|
We can use Morris Traversal to traverse all the nodes of the binary tree in O(n) time complexity but with O(1) space complexity.
Advantages of Binary Tree
- Efficient Search: Binary trees are efficient when searching for a specific element, as each node has at most two child nodes, allowing for binary search algorithms to be used.
- Memory Efficient: Binary trees require lesser memory as compared to other tree data structures, therefore they are memory-efficient.
- Binary trees are relatively easy to implement and understand as each node has at most two children, left child and right child.
Disadvantages of Binary Tree
- Limited structure: Binary trees are limited to two child nodes per node, which can limit their usefulness in certain applications. For example, if a tree requires more than two child nodes per node, a different tree structure may be more suitable.
- Unbalanced trees: Unbalanced binary trees, where one subtree is significantly larger than the other, can lead to inefficient search operations. This can occur if the tree is not properly balanced or if data is inserted in a non-random order.
- Space inefficiency: Binary trees can be space inefficient when compared to other data structures. This is because each node requires two child pointers, which can be a significant amount of memory overhead for large trees.
- Slow performance in worst-case scenarios: In the worst-case scenario, a binary tree can become degenerate or skewed, meaning that each node has only one child. In this case, search operations can degrade to O(n) time complexity, where n is the number of nodes in the tree.
Applications of Binary Tree
- Binary Tree can be used to represent hierarchical data.
- Huffman Coding trees are used in data compression algorithms.
- Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
- Useful for indexing segmented at the database is useful in storing cache in the system,
- Binary trees can be used to implement decision trees, a type of machine learning algorithm used for classification and regression analysis.
Frequently Asked Questions on Binary Tree
1. What is a binary tree?
A binary tree is a non-linear data structure consisting of nodes, where each node has at most two children (left child and the right child).
2. What are the types of binary trees?
Binary trees can be classified into various types, including full binary trees, complete binary trees, perfect binary trees, balanced binary trees (such as AVL trees and Red-Black trees), and degenerate (or pathological) binary trees.
3. What is the height of a binary tree?
The height of a binary tree is the length of the longest path from the root node to a leaf node. It represents the number of edges in the longest path from the root node to a leaf node.
4. What is the depth of a node in a binary tree?
The depth of a node in a binary tree is the length of the path from the root node to that particular node. The depth of the root node is 0.
5. How do you perform tree traversal in a binary tree?
Tree traversal in a binary tree can be done in different ways: In-order traversal, Pre-order traversal, Post-order traversal, and Level-order traversal (also known as breadth-first traversal).
6. What is an Inorder traversal in Binary Tree?
In Inorder traversal, nodes are recursively visited in this order: left child, root, right child. This traversal results in nodes being visited in non-decreasing order in a binary search tree.
7. What is a Preorder traversal in Binary Tree?
In Preorder traversal, nodes are recursively visited in this order: root, left child, right child. This traversal results in root node being the first node to be visited.
8. What is a Postorder traversal in Binary Tree?
In Postorder traversal, nodes are recursively visited in this order: left child, right child and root. This traversal results in root node being the last node to be visited.
9. What is the difference between a Binary Tree and a Binary Search Tree?
A binary tree is a hierarchical data structure where each node has at most two children, whereas a binary search tree is a type of binary tree in which the left child of a node contains values less than the node’s value, and the right child contains values greater than the node’s value.
10. What is a balanced binary tree?
A balanced binary tree is a binary tree in which the height of the left and right subtrees of every node differ by at most one. Balanced trees help maintain efficient operations such as searching, insertion, and deletion with time complexities close to O(log n).
Conclusion:
Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.
Related Articles:
Please Login to comment...