Implement Stack using Queues
Last Updated :
23 May, 2024
Given a Queue data structure that supports standard operations like enqueue() and dequeue(). The task is to implement a Stack data structure using only instances of Queue and Queue operations allowed on the instances.
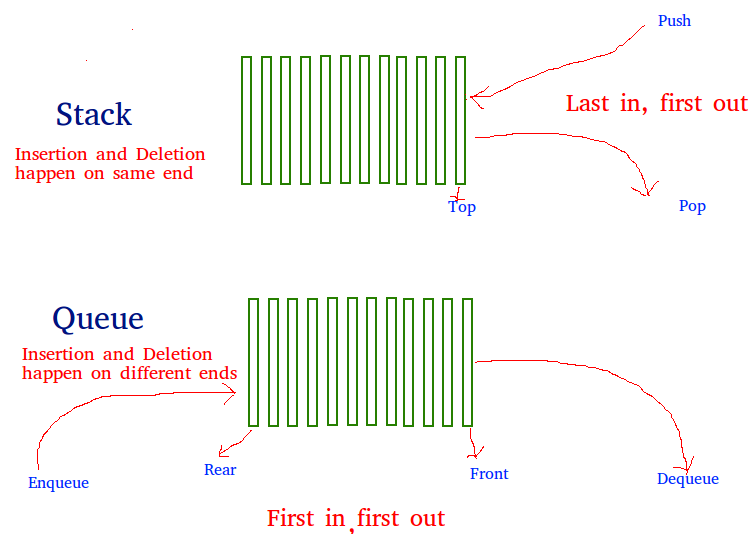
A Stack can be implemented using two queues. Let Stack to be implemented be ‘s’ and queues used to implement are ‘q1’ and ‘q2’. Stack ‘s’ can be implemented in two ways:
Implement Stack using Queues By making push() operation costly:
Below is the idea to solve the problem:
The idea is to keep newly entered element at the front of ‘q1’ so that pop operation dequeues from ‘q1’. ‘q2’ is used to put every new element in front of ‘q1’.
- Follow the below steps to implement the push(s, x) operation:
- Enqueue x to q2.
- One by one dequeue everything from q1 and enqueue to q2.
- Swap the queues of q1 and q2.
- Follow the below steps to implement the pop(s) operation:
- Dequeue an item from q1 and return it.
Below is the implementation of the above approach.
C++
/* Program to implement a stack using
two queue */
#include <bits/stdc++.h>
using namespace std;
class Stack {
// Two inbuilt queues
queue<int> q1, q2;
public:
void push(int x)
{
// Push x first in empty q2
q2.push(x);
// Push all the remaining
// elements in q1 to q2.
while (!q1.empty()) {
q2.push(q1.front());
q1.pop();
}
// swap the names of two queues
queue<int> q = q1;
q1 = q2;
q2 = q;
}
void pop()
{
// if no elements are there in q1
if (q1.empty())
return;
q1.pop();
}
int top()
{
if (q1.empty())
return -1;
return q1.front();
}
int size() { return q1.size(); }
};
// Driver code
int main()
{
Stack s;
s.push(1);
s.push(2);
s.push(3);
cout << "current size: " << s.size() << endl;
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
cout << "current size: " << s.size() << endl;
return 0;
}
// This code is contributed by Chhavi
/* Java Program to implement a stack using
two queue */
import java.util.*;
class GfG {
static class Stack {
// Two inbuilt queues
static Queue<Integer> q1
= new LinkedList<Integer>();
static Queue<Integer> q2
= new LinkedList<Integer>();
// To maintain current number of
// elements
static int curr_size;
static void push(int x)
{
// Push x first in empty q2
q2.add(x);
// Push all the remaining
// elements in q1 to q2.
while (!q1.isEmpty()) {
q2.add(q1.peek());
q1.remove();
}
// swap the names of two queues
Queue<Integer> q = q1;
q1 = q2;
q2 = q;
}
static void pop()
{
// if no elements are there in q1
if (q1.isEmpty())
return;
q1.remove();
}
static int top()
{
if (q1.isEmpty())
return -1;
return q1.peek();
}
static int size() { return q1.size(); }
}
// driver code
public static void main(String[] args)
{
Stack s = new Stack();
s.push(1);
s.push(2);
s.push(3);
System.out.println("current size: " + s.size());
System.out.println(s.top());
s.pop();
System.out.println(s.top());
s.pop();
System.out.println(s.top());
System.out.println("current size: " + s.size());
}
}
// This code is contributed by Prerna
# Program to implement a stack using
# two queue
from _collections import deque
class Stack:
def __init__(self):
# Two inbuilt queues
self.q1 = deque()
self.q2 = deque()
def push(self, x):
# Push x first in empty q2
self.q2.append(x)
# Push all the remaining
# elements in q1 to q2.
while (self.q1):
self.q2.append(self.q1.popleft())
# swap the names of two queues
self.q1, self.q2 = self.q2, self.q1
def pop(self):
# if no elements are there in q1
if self.q1:
self.q1.popleft()
def top(self):
if (self.q1):
return self.q1[0]
return None
def size(self):
return len(self.q1)
# Driver Code
if __name__ == '__main__':
s = Stack()
s.push(1)
s.push(2)
s.push(3)
print("current size: ", s.size())
print(s.top())
s.pop()
print(s.top())
s.pop()
print(s.top())
print("current size: ", s.size())
# This code is contributed by PranchalK
/* C# Program to implement a stack using
two queue */
using System;
using System.Collections;
class GfG {
public class Stack {
// Two inbuilt queues
public Queue q1 = new Queue();
public Queue q2 = new Queue();
public void push(int x)
{
// Push x first in empty q2
q2.Enqueue(x);
// Push all the remaining
// elements in q1 to q2.
while (q1.Count > 0) {
q2.Enqueue(q1.Peek());
q1.Dequeue();
}
// swap the names of two queues
Queue q = q1;
q1 = q2;
q2 = q;
}
public void pop()
{
// if no elements are there in q1
if (q1.Count == 0)
return;
q1.Dequeue();
}
public int top()
{
if (q1.Count == 0)
return -1;
return (int)q1.Peek();
}
public int size() { return q1.Count; }
};
// Driver code
public static void Main(String[] args)
{
Stack s = new Stack();
s.push(1);
s.push(2);
s.push(3);
Console.WriteLine("current size: " + s.size());
Console.WriteLine(s.top());
s.pop();
Console.WriteLine(s.top());
s.pop();
Console.WriteLine(s.top());
Console.WriteLine("current size: " + s.size());
}
}
// This code is contributed by Arnab Kundu
/*Javascript Program to implement a stack using
two queue */
// Two inbuilt queues
class Stack {
constructor() {
this.q1 = [];
this.q2 = [];
}
push(x) {
// Push x first in isEmpty q2
this.q2.push(x);
// Push all the remaining
// elements in q1 to q2.
while (this.q1.length != 0) {
this.q2.push(this.q1[0]);
this.q1.shift();
}
// swap the names of two queues
this.q = this.q1;
this.q1 = this.q2;
this.q2 = this.q;
}
pop() {
// if no elements are there in q1
if (this.q1.length == 0)
return;
this.q1.shift();
}
top() {
if (this.q1.length == 0)
return -1;
return this.q1[0];
}
size() {
console.log(this.q1.length);
}
isEmpty() {
// return true if the queue is empty.
return this.q1.length == 0;
}
front() {
return this.q1[0];
}
}
// Driver code
let s = new Stack();
s.push(1);
s.push(2);
s.push(3);
console.log("current size: ");
s.size();
console.log(s.top());
s.pop();
console.log(s.top());
s.pop();
console.log(s.top());
console.log("current size: ");
s.size();
// This code is contributed by adityamaharshi21
Outputcurrent size: 3
3
2
1
current size: 1
Time Complexity:
- Push operation: O(N), As all the elements need to be popped out from the Queue (q1) and push them back to Queue (q2).
- Pop operation: O(1), As we need to remove the front element from the Queue.
Auxiliary Space: O(N), As we use two queues for the implementation of a Stack.
Implement Stack using Queues by making pop() operation costly:
Below is the idea to solve the problem:
The new element is always enqueued to q1. In pop() operation, if q2 is empty then all the elements except the last, are moved to q2. Finally, the last element is dequeued from q1 and returned.
- Follow the below steps to implement the push(s, x) operation:
- Enqueue x to q1 (assuming the size of q1 is unlimited).
- Follow the below steps to implement the pop(s) operation:
- One by one dequeue everything except the last element from q1 and enqueue to q2.
- Dequeue the last item of q1, the dequeued item is the result, store it.
- Swap the names of q1 and q2
- Return the item stored in step 2.
Below is the implementation of the above approach:
C++
// Program to implement a stack
// using two queue
#include <bits/stdc++.h>
using namespace std;
class Stack {
queue<int> q1, q2;
public:
void pop()
{
if (q1.empty())
return;
// Leave one element in q1 and
// push others in q2.
while (q1.size() != 1) {
q2.push(q1.front());
q1.pop();
}
// Pop the only left element
// from q1
q1.pop();
// swap the names of two queues
queue<int> q = q1;
q1 = q2;
q2 = q;
}
void push(int x) { q1.push(x); }
int top()
{
if (q1.empty())
return -1;
while (q1.size() != 1) {
q2.push(q1.front());
q1.pop();
}
// last pushed element
int temp = q1.front();
// to empty the auxiliary queue after
// last operation
q1.pop();
// push last element to q2
q2.push(temp);
// swap the two queues names
queue<int> q = q1;
q1 = q2;
q2 = q;
return temp;
}
int size() { return q1.size(); }
};
// Driver code
int main()
{
Stack s;
s.push(1);
s.push(2);
s.push(3);
cout << "current size: " << s.size() << endl;
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
cout << "current size: " << s.size() << endl;
return 0;
}
// This code is contributed by Chhavi
/* Java Program to implement a stack
using two queue */
import java.util.*;
class Stack {
Queue<Integer> q1 = new LinkedList<>(),
q2 = new LinkedList<>();
void remove()
{
if (q1.isEmpty())
return;
// Leave one element in q1 and
// push others in q2.
while (q1.size() != 1) {
q2.add(q1.peek());
q1.remove();
}
// Pop the only left element
// from q1
q1.remove();
// swap the names of two queues
Queue<Integer> q = q1;
q1 = q2;
q2 = q;
}
void add(int x) { q1.add(x); }
int top()
{
if (q1.isEmpty())
return -1;
while (q1.size() != 1) {
q2.add(q1.peek());
q1.remove();
}
// last pushed element
int temp = q1.peek();
// to empty the auxiliary queue after
// last operation
q1.remove();
// push last element to q2
q2.add(temp);
// swap the two queues names
Queue<Integer> q = q1;
q1 = q2;
q2 = q;
return temp;
}
int size() { return q1.size(); }
// Driver code
public static void main(String[] args)
{
Stack s = new Stack();
s.add(1);
s.add(2);
s.add(3);
System.out.println("current size: " + s.size());
System.out.println(s.top());
s.remove();
System.out.println(s.top());
s.remove();
System.out.println(s.top());
System.out.println("current size: " + s.size());
}
}
// This code is contributed by Princi Singh
# Program to implement a stack using
# two queue
from _collections import deque
class Stack:
def __init__(self):
# Two inbuilt queues
self.q1 = deque()
self.q2 = deque()
def push(self, x):
self.q1.append(x)
def pop(self):
# if no elements are there in q1
if (not self.q1):
return
# Leave one element in q1 and push others in q2
while(len(self.q1) != 1):
self.q2.append(self.q1.popleft())
# swap the names of two queues
self.q1, self.q2 = self.q2, self.q1
def top(self):
# if no elements are there in q1
if (not self.q1):
return
# Leave one element in q1 and push others in q2
while(len(self.q1) != 1):
self.q2.append(self.q1.popleft())
# Pop the only left element from q1 to q2
top = self.q1[0]
self.q2.append(self.q1.popleft())
# swap the names of two queues
self.q1, self.q2 = self.q2, self.q1
return top
def size(self):
return len(self.q1)
# Driver Code
if __name__ == '__main__':
s = Stack()
s.push(1)
s.push(2)
s.push(3)
print("current size: ", s.size())
print(s.top())
s.pop()
print(s.top())
s.pop()
print(s.top())
print("current size: ", s.size())
# This code is contributed by jainlovely450
using System;
using System.Collections;
class GfG {
public class Stack {
public Queue q1 = new Queue();
public Queue q2 = new Queue();
// Just enqueue the new element to q1
public void Push(int x) = > q1.Enqueue(x);
// move all elements from q1 to q2 except the rear
// of q1. Store the rear of q1 swap q1 and q2 return
// the stored result
public int Pop()
{
if (q1.Count == 0)
return -1;
while (q1.Count > 1) {
q2.Enqueue(q1.Dequeue());
}
int res = (int)q1.Dequeue();
Queue temp = q1;
q1 = q2;
q2 = temp;
return res;
}
public int Size() = > q1.Count;
public int Top()
{
if (q1.Count == 0)
return -1;
while (q1.Count > 1) {
q2.Enqueue(q1.Dequeue());
}
int res = (int)q1.Dequeue();
q2.Enqueue(res);
Queue temp = q1;
q1 = q2;
q2 = temp;
return res;
}
};
public static void Main(String[] args)
{
Stack s = new Stack();
s.Push(1);
s.Push(2);
s.Push(3);
Console.WriteLine("current size: " + s.Size());
Console.WriteLine(s.Top());
s.Pop();
Console.WriteLine(s.Top());
s.Pop();
Console.WriteLine(s.Top());
Console.WriteLine("current size: " + s.Size());
}
}
// Submitted by Sakti Prasad
/*Javascript Program to implement a stack using
two queue */
// Two inbuilt queues
class Stack {
constructor() {
this.q1 = [];
this.q2 = [];
}
pop()
{
if (this.q1.length == 0)
return;
// Leave one element in q1 and
// push others in q2.
while (this.q1.length != 1){
this.q2.push(this.q1[0]);
this.q1.shift();
}
// Pop the only left element
// from q1f
this.q1.shift();
// swap the names of two queues
this.q = this.q1;
this.q1 = this.q2;
this.q2 = this.q;
}
push(x) {
// if no elements are there in q1
this.q1.push(x);
}
top() {
if (this.q1.length == 0)
return -1;
while (this.q1.length != 1) {
this.q2.push(this.q1[0]);
this.q1.shift();
}
// last pushed element
let temp = this.q1[0];
// to empty the auxiliary queue after
// last operation
this.q1.shift();
// push last element to q2
this.q2.push(temp);
// swap the two queues names
this.q = this.q1;
this.q1 = this.q2;
this.q2 = this.q;
return temp;
}
size() {
console.log(this.q1.length);
}
isEmpty() {
// return true if the queue is empty.
return this.q1.length == 0;
}
front() {
return this.q1[0];
}
}
// Driver code
let s = new Stack();
s.push(1);
s.push(2);
s.push(3);
console.log("current size: ");
s.size();
console.log(s.top());
s.pop();
console.log(s.top());
s.pop();
console.log(s.top());
console.log("current size: ");
s.size();
// This code is contributed by Susobhan Akhuli
Outputcurrent size: 3
3
2
1
current size: 1
Time Complexity:
- Push operation: O(1), As, on each push operation the new element is added at the end of the Queue.
- Pop operation: O(N), As, on each pop operation, all the elements are popped out from the Queue (q1) except the last element and pushed into the Queue (q2).
Auxiliary Space: O(N) since 2 queues are used.
Implement Stack using 1 queue:
Below is the idea to solve the problem:
Using only one queue and make the queue act as a Stack in modified way of the above discussed approach.
Follow the below steps to implement the idea:
- The idea behind this approach is to make one queue and push the first element in it.
- After the first element, we push the next element and then push the first element again and finally pop the first element.
- So, according to the FIFO rule of the queue, the second element that was inserted will be at the front and then the first element as it was pushed again later and its first copy was popped out.
- So, this acts as a Stack and we do this at every step i.e. from the initial element to the second last element, and the last element will be the one that we are inserting and since we will be pushing the initial elements after pushing the last element, our last element becomes the first element.
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
// Stack Class that acts as a queue
class Stack {
queue<int> q;
public:
void push(int data);
void pop();
int top();
int size();
bool empty();
};
// Push operation
void Stack::push(int data)
{
// Get previous size of queue
int s = q.size();
// Push the current element
q.push(data);
// Pop all the previous elements and put them after
// current element
for (int i = 0; i < s; i++) {
// Add the front element again
q.push(q.front());
// Delete front element
q.pop();
}
}
// Removes the top element
void Stack::pop()
{
if (q.empty())
cout << "No elements\n";
else
q.pop();
}
// Returns top of stack
int Stack::top() { return (q.empty()) ? -1 : q.front(); }
// Returns true if Stack is empty else false
bool Stack::empty() { return (q.empty()); }
int Stack::size() { return q.size(); }
int main()
{
Stack st;
st.push(1);
st.push(2);
st.push(3);
cout << "current size: " << st.size() << "\n";
cout << st.top() << "\n";
st.pop();
cout << st.top() << "\n";
st.pop();
cout << st.top() << "\n";
cout << "current size: " << st.size();
return 0;
}
import java.util.*;
/* Java Program to implement a stack
using only one queue */
class Stack {
// One queue
Queue<Integer> q1 = new LinkedList<Integer>();
void push(int x)
{
// Get previous size of queue
int s = q1.size();
// Push the current element
q1.add(x);
// Pop all the previous elements and put them after
// current element
for (int i = 0; i < s; i++) {
q1.add(q1.remove());
}
}
void pop()
{
// if no elements are there in q1
if (q1.isEmpty())
return;
q1.remove();
}
int top()
{
if (q1.isEmpty())
return -1;
return q1.peek();
}
int size() { return q1.size(); }
// driver code
public static void main(String[] args)
{
Stack s = new Stack();
s.push(1);
s.push(2);
s.push(3);
System.out.println("current size: " + s.size());
System.out.println(s.top());
s.pop();
System.out.println(s.top());
s.pop();
System.out.println(s.top());
System.out.println("current size: " + s.size());
}
}
// This code is contributed by Vishal Singh Shekhawat
from _collections import deque
# Stack Class that acts as a queue
class Stack:
def __init__(self):
self.q = deque()
# Push operation
def push(self, data):
# Get previous size of queue
s = len(self.q)
# Push the current element
self.q.append(data)
# Pop all the previous elements and put them after
# current element
for i in range(s):
self.q.append(self.q.popleft())
# Removes the top element
def pop(self):
if (not self.q):
print("No elements")
else:
self.q.popleft()
# Returns top of stack
def top(self):
if (not self.q):
return
return self.q[0]
def size(self):
return len(self.q)
if __name__ == '__main__':
st = Stack()
st.push(1)
st.push(2)
st.push(3)
print("current size: ", st.size())
print(st.top())
st.pop()
print(st.top())
st.pop()
print(st.top())
print("current size: ", st.size())
/* C# Program to implement a stack using only one queue */
using System;
using System.Collections;
class GfG {
public class Stack
{
// One inbuilt queue
public Queue q = new Queue();
public void push(int x)
{
// Get previous size of queue
int s = q.Count;
// Push the current element
q.Enqueue(x);
// Pop all the previous elements and put them
// afte current element
for (int i = 0; i < s; i++) {
// Add the front element again
q.Enqueue(q.Peek());
// Delete front element
q.Dequeue();
}
}
// Removes the top element
public void pop()
{
// if no elements are there in q
if (q.Count == 0)
Console.WriteLine("No elements");
else
q.Dequeue();
}
// Returns top of stack
public int top()
{
if (q.Count == 0)
return -1;
return (int)q.Peek();
}
public int size() { return q.Count; }
};
// Driver code
public static void Main(String[] args)
{
Stack st = new Stack();
st.push(1);
st.push(2);
st.push(3);
Console.WriteLine("current size: " + st.size());
Console.WriteLine(st.top());
st.pop();
Console.WriteLine(st.top());
st.pop();
Console.WriteLine(st.top());
Console.WriteLine("current size: " + st.size());
}
}
// This code is contributed by Susobhan Akhuli
/*Javascript Program to implement a stack using
only one queue */
// One inbuilt queue
class Stack {
constructor() {
this.q = [];
}
// Push operation
push(data) {
// Get previous size of queue
let s = this.q.length;
// Push the current element
this.q.push(data);
// Pop all the previous elements and put them after
// current element
for (let i = 0; i < s; i++) {
// Add the front element again
this.q.push(this.q[0]);
// Delete front element
this.q.shift();
}
}
// Removes the top element
pop() {
// if no elements are there in q1
if (this.q.length == 0)
console.log("No elements");
else
this.q.shift();
}
top() {
if (this.q.length == 0)
return -1;
return this.q[0];
}
size() {
console.log(this.q.length);
}
isEmpty() {
// return true if the queue is empty.
return this.q.length == 0;
}
front() {
return this.q[0];
}
}
// Driver code
let st = new Stack();
st.push(1);
st.push(2);
st.push(3);
console.log("current size: ");
st.size();
console.log(st.top());
st.pop();
console.log(st.top());
st.pop();
console.log(st.top());
console.log("current size: ");
st.size();
// This code is contributed by Susobhan Akhuli
Outputcurrent size: 3
3
2
1
current size: 1
Time Complexity:
- Push operation: O(N)
- Pop operation: O(1)
Auxiliary Space: O(N) since 1 queue is used.
Recursive Method:
Below is the implementation for the above approach using recursion –
C++
// CPP Program to implement a stack
// using one queue and recursion
#include <bits/stdc++.h>
using namespace std;
// Stack Class that acts as a queue
class Stack {
queue<int> q;
public:
void push(int data, int c);
void pop();
int top();
int size();
bool empty();
};
// Push operation
void Stack::push(int data, int c)
{
// Push the current element first and
// After every recursion add the front element again
q.push(data);
// Return if size becomes 0
if (c <= 0)
return;
// Store current front
int x = q.front();
// Delete front element
q.pop();
// Decrement size by 1 in every recursion
c--;
Stack::push(x, c);
}
// Removes the top element
void Stack::pop()
{
if (q.empty())
cout << "No elements\n";
else
q.pop();
}
// Returns top of stack
int Stack::top() { return (q.empty()) ? -1 : q.front(); }
// Returns true if Stack is empty else false
bool Stack::empty() { return (q.empty()); }
int Stack::size() { return q.size(); }
int main()
{
Stack st;
st.push(1, st.size()); // Value and size
st.push(2, st.size());
st.push(3, st.size());
cout << "current size: " << st.size() << "\n";
cout << st.top() << "\n";
st.pop();
cout << st.top() << "\n";
st.pop();
cout << st.top() << "\n";
cout << "current size: " << st.size();
return 0;
}
// This code is contributed by Susobhan Akhuli
import java.util.*;
/* Java Program to implement a stack
using only one queue */
class Stack {
// One queue
Queue<Integer> q1 = new LinkedList<Integer>();
void push(int data, int c)
{
// Push the current element first and
// After every recursion add the front element again
q1.add(data);
// Return if size becomes 0
if (c <= 0)
return;
// Decrement size by 1 in every recursion
c--;
// remove front element from queue and return it
// using q1.remove() and call recursive function
push(q1.remove(), c);
}
void pop()
{
// if no elements are there in q1
if (q1.isEmpty())
return;
q1.remove();
}
int top()
{
if (q1.isEmpty())
return -1;
return q1.peek();
}
int size() { return q1.size(); }
// driver code
public static void main(String[] args)
{
Stack s = new Stack();
s.push(1, s.size()); // Value and current size
s.push(2, s.size());
s.push(3, s.size());
System.out.println("current size: " + s.size());
System.out.println(s.top());
s.pop();
System.out.println(s.top());
s.pop();
System.out.println(s.top());
System.out.println("current size: " + s.size());
}
}
// This code is contributed by Susobhan Akhuli
from _collections import deque
# Stack Class that acts as a queue
class Stack:
def __init__(self):
self.q = deque()
# Push operation
def push(self, data, c):
# Push the current element
self.q.append(data)
# Return if size becomes 0
if c <= 0:
return
# Store and then pop the current front
x = self.q.popleft()
# Decrement size by 1 in every recursion
c = c-1
self.push(x, c)
# Removes the top element
def pop(self):
if (not self.q):
print("No elements")
else:
self.q.popleft()
# Returns top of stack
def top(self):
if (not self.q):
return
return self.q[0]
def size(self):
return len(self.q)
if __name__ == '__main__':
st = Stack()
st.push(1, st.size())
st.push(2, st.size())
st.push(3, st.size())
print("current size: ", st.size())
print(st.top())
st.pop()
print(st.top())
st.pop()
print(st.top())
print("current size: ", st.size())
# This code is contributed by Susobhan Akhuli
// C# Program to implement a stack
// using one queue and recursion
using System;
using System.Collections;
class GfG {
public class Stack {
// One inbuilt queue
public Queue q = new Queue();
// Push operation
public void push(int x, int c)
{
// Push the current element first and
// After every recursion add the front element
// again
q.Enqueue(x);
// Return if size becomes 0
if (c <= 0)
return;
// Store current front
int p = (int)q.Peek();
// Delete front element
q.Dequeue();
// Decrement size by 1 in every recursion
c--;
push(p, c);
}
// Removes the top element
public void pop()
{
// if no elements are there in q
if (q.Count == 0)
Console.WriteLine("No elements");
else
q.Dequeue();
}
// Returns top of stack
public int top()
{
if (q.Count == 0)
return -1;
return (int)q.Peek();
}
public int size() { return q.Count; }
};
// Driver code
public static void Main(String[] args)
{
Stack st = new Stack();
st.push(1, st.size());
st.push(2, st.size());
st.push(3, st.size());
Console.WriteLine("current size: " + st.size());
Console.WriteLine(st.top());
st.pop();
Console.WriteLine(st.top());
st.pop();
Console.WriteLine(st.top());
Console.WriteLine("current size: " + st.size());
}
}
// This code is contributed by Susobhan Akhuli
// Javascript Program to implement a stack using one queue and recursion
// Stack Class that acts as a queue
class Stack {
constructor() {
this.q = [];
}
// Push operation
push(data, c) {
// Push the current element first and
//After every recursion add the front element again
this.q.push(data);
//Returns if size becomes 0
if (c <= 0) {
return;
}
//Store Current Front
let x = this.q[0];
//Delete front element
this.q.shift();
//Decrease size by 1 in every recursion
c--;
this.push(x, c);
}
// Removes the top element
pop() {
if (this.q.length == 0) console.log("No elements");
else this.q.shift();
}
//Return top of stack
top() {
if (this.q.length == 0) return -1;
return this.q[0];
}
// return true if the stack is empty else false.
isEmpty() {
return this.q.length == 0;
}
size() {
return this.q.length;
}
}
// Driver code
let st = new Stack();
st.push(1, st.size()); //value and size
st.push(2, st.size());
st.push(3, st.size());
console.log("current size: " + st.size());
console.log(st.top());
st.pop();
console.log(st.top());
st.pop();
console.log(st.top());
console.log("current size: " + st.size());
// This code is contributed by satwiksuman.
Outputcurrent size: 3
3
2
1
current size: 1
Time Complexity:
- Push operation: O(N)
- Pop operation: O(1)
Auxiliary Space: O(N) since 1 queue is used and also for the stack used for recursion.
Additional Methods:
- Using a Deque (Double Ended Queue):
A Deque is a data structure that supports adding and removing elements from both ends in constant time. To implement a Stack using a Deque, we can make use of the addFirst and removeFirst methods to implement push and pop operations respectively.
C++
// CPP Program to implement a stack
// using dequeue
#include <bits/stdc++.h>
using namespace std;
class Stack {
private:
// Create an empty deque
deque<int> my_deque;
public:
void push(int item)
{
// Append the item to the end of the deque
my_deque.push_back(item);
}
int pop()
{
// Remove and return the item from the end of the
// deque
int item = my_deque.back();
my_deque.pop_back();
return item;
}
int size()
{
// Return size of deque
return my_deque.size();
}
bool is_empty()
{
// Return True if the deque is empty, and False
// otherwise
return my_deque.empty();
}
int top()
{
if (is_empty()) {
// If the stack is empty, return -1
return -1;
}
else {
// Return the last item in the deque
return my_deque.back();
}
}
};
int main()
{
Stack st;
st.push(1);
st.push(2);
st.push(3);
cout << "current size: " << st.size() << endl;
cout << st.top() << endl;
st.pop();
cout << st.top() << endl;
st.pop();
cout << st.top() << endl;
cout << "current size: " << st.size() << endl;
return 0;
}
// This code is contributed by Susobhan Akhuli
// Java program to implement a stack using Deque
import java.util.*;
class Stack {
// Create an empty deque
Deque<Integer> myDeque = new LinkedList<>();
void push(int item) {
// Append the item to the end of the deque
myDeque.addLast(item);
}
int pop() {
// Remove and return the item from the end of the deque
int item = myDeque.getLast();
myDeque.removeLast();
return item;
}
int size() {
// Return size of deque
return myDeque.size();
}
boolean isEmpty() {
// Return true if the deque is empty, and false otherwise
return myDeque.isEmpty();
}
int top() {
if (isEmpty()) {
// If the stack is empty, return -1
return -1;
}
else {
// Return the last item in the deque
return myDeque.getLast();
}
}
}
class GFG {
public static void main(String[] args) {
Stack st = new Stack();
st.push(1);
st.push(2);
st.push(3);
System.out.println("current size: " + st.size());
System.out.println(st.top());
st.pop();
System.out.println(st.top());
st.pop();
System.out.println(st.top());
System.out.println("current size: " + st.size());
}
}
// This code is contributed by Susobhan Akhuli
# Python Program to implement a stack
# using dequeue
from collections import deque
# Define the Stack class
class Stack:
def __init__(self):
# Create an empty dequeue
self.dequeue = deque()
def push(self, item):
# Append the item to the end of the dequeue
self.dequeue.append(item)
def pop(self):
# Remove and return the item from the end of the dequeue
return self.dequeue.pop()
def size(self):
# Return size of dequeue
return len(self.dequeue)
def is_empty(self):
# Return True if the dequeue is empty, and False otherwise
return not self.dequeue
def top(self):
# Return the item at the top of the stack without removing it.
if self.is_empty():
# If the stack is empty, return None
return None
else:
# Return the last item in the dequeue
return self.dequeue[-1]
if __name__ == '__main__':
st = Stack()
st.push(1)
st.push(2)
st.push(3)
print("current size:", st.size())
print(st.top())
st.pop()
print(st.top())
st.pop()
print(st.top())
print("current size:", st.size())
# This code is contributed by Susobhan Akhuli
// C# Program to implement a stack
// using dequeue
using System;
using System.Collections.Generic;
class Stack {
private LinkedList<int> list = new LinkedList<int>();
public void Push(int item)
{
// Append the item to the end of the linked list
list.AddLast(item);
}
public int Pop()
{
// Remove and return the item from the end of the
// linked list
int item = list.Last.Value;
list.RemoveLast();
return item;
}
public int Size()
{
// Return the size of the linked list
return list.Count;
}
public bool IsEmpty()
{
// Return true if the linked list is empty, and
// false otherwise
return list.Count == 0;
}
public int Top()
{
if (IsEmpty()) {
// If the stack is empty, return -1
return -1;
}
else {
// Return the last item in the linked list
return list.Last.Value;
}
}
}
class Program {
static void Main(string[] args)
{
Stack st = new Stack();
st.Push(1);
st.Push(2);
st.Push(3);
Console.WriteLine("current size: " + st.Size());
Console.WriteLine(st.Top());
st.Pop();
Console.WriteLine(st.Top());
st.Pop();
Console.WriteLine(st.Top());
Console.WriteLine("current size: " + st.Size());
}
}
// This code is contributed by Susobhan Akhuli
<script>
// JavaScript Program to implement a stack
// using dequeue
// Define the Stack class
class Stack {
constructor() {
// Create an empty dequeue
this.dequeue = [];
}
push(item) {
// Append the item to the end of the dequeue
this.dequeue.push(item);
}
pop() {
// Remove and return the item from the end of the dequeue
return this.dequeue.pop();
}
size() {
// Return size of dequeue
return this.dequeue.length;
}
is_empty() {
// Return True if the dequeue is empty, and False otherwise
return this.dequeue.length == 0;
}
top() {
// Return the item at the top of the stack without removing it.
if (this.is_empty()) {
// If the stack is empty, return None
return null;
} else {
// Return the last item in the dequeue
return this.dequeue[this.dequeue.length - 1];
}
}
}
let st = new Stack();
st.push(1);
st.push(2);
st.push(3);
console.log("current size: " + st.size());
console.log(st.top());
st.pop();
console.log(st.top());
st.pop();
console.log(st.top());
console.log("current size: " + st.size());
// This code is contributed by Susobhan Akhuli
</script>
Outputcurrent size: 3
3
2
1
current size: 1
- Using a Circular Queue:
In this method, we use a Circular Queue to implement the Stack. We keep track of the front and rear indices, and whenever we need to push an element, we simply increase the rear index and add the element to the rear position. To pop an element, we simply decrease the rear index.
C++
// CPP program for above approach
#include <bits/stdc++.h>
using namespace std;
class Stack {
// Indices to keep track of the front, rear and size of
// the queue
int front, rear, size;
// Maximum capacity of the queue
unsigned capacity;
// Pointer to the array used to store the elements
int* arr;
public:
Stack(unsigned capacity)
{
this->capacity = capacity;
// Initially, front index and size are set to 0
front = size = 0;
// Rear index is set to the last index of the array
rear = capacity - 1;
// Dynamic allocation of memory for the array
arr = new int[this->capacity];
}
bool isFull()
{
// If size is equal to the capacity, the queue is
// full
return (size == capacity);
}
bool isEmpty()
{
// If size is 0, the queue is empty
return (size == 0);
}
void push(int x)
{
if (isFull())
// If the queue is full, return without adding
// the element
return;
// Increase the rear index by 1 (with wraparound)
rear = (rear + 1) % capacity;
// Add the element to the rear position
arr[rear] = x;
// Increase the size of the queue by 1
size++;
}
void pop()
{
if (isEmpty())
return; // If the queue is empty, return without
// doing anything
// Increase the front index by 1 (with wraparound)
front = (front + 1) % capacity;
// Decrease the size of the queue by 1
size--;
}
int top()
{
if (isEmpty())
// If the queue is empty, return -1
return -1;
// Return the element at the front position
return arr[front];
}
int getSize()
{
// Return the current size of the queue
return size;
}
};
int main()
{
// Create a stack of maximum size 3
Stack s(3);
s.push(1);
s.push(2);
s.push(3);
cout << "current size: " << s.getSize() << endl;
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
s.pop();
cout << s.top() << endl;
cout << "current size: " << s.getSize() << endl;
return 0;
}
// This code is contributed by Susobhan Akhuli
// Java program for above approach
import java.util.*;
class Stack {
// Indices to keep track of the front, rear and size of
// the queue
private int front, rear, size;
// Maximum capacity of the queue
private int capacity;
// Array used to store the elements
private int[] arr;
public Stack(int capacity)
{
this.capacity = capacity;
// Initially, front index and size are set to 0
front = size = 0;
// Rear index is set to the last index of the array
rear = capacity - 1;
// Dynamic allocation of memory for the array
arr = new int[this.capacity];
}
public boolean isFull()
{
// If size is equal to the capacity, the queue is
// full
return (size == capacity);
}
public boolean isEmpty()
{
// If size is 0, the queue is empty
return (size == 0);
}
public void push(int x)
{
if (isFull())
// If the queue is full, return without adding
// the element
return;
// Increase the rear index by 1 (with wraparound)
rear = (rear + 1) % capacity;
// Add the element to the rear position
arr[rear] = x;
// Increase the size of the queue by 1
size++;
}
public void pop()
{
if (isEmpty())
return; // If the queue is empty, return without
// doing anything
// Increase the front index by 1 (with wraparound)
front = (front + 1) % capacity;
// Decrease the size of the queue by 1
size--;
}
public int top()
{
if (isEmpty())
// If the queue is empty, return -1
return -1;
// Return the element at the front position
return arr[front];
}
public int getSize()
{
// Return the current size of the queue
return size;
}
}
public class GFG {
public static void main(String[] args) {
// Create a stack of maximum size 3
Stack s = new Stack(3);
s.push(1);
s.push(2);
s.push(3);
System.out.println("current size: " + s.getSize());
System.out.println(s.top());
s.pop();
System.out.println(s.top());
s.pop();
System.out.println(s.top());
System.out.println("current size: " + s.getSize());
}
}
// This code is contributed by Susobhan Akhuli
class Stack:
def __init__(self, capacity):
# Initialize the stack with the given capacity
self.capacity = capacity
self.front = self.size = 0
self.rear = capacity - 1
# Create an array to store the elements of the stack
self.arr = [0] * self.capacity
def isFull(self):
# Check if the stack is full
return self.size == self.capacity
def isEmpty(self):
# Check if the stack is empty
return self.size == 0
def push(self, x):
if self.isFull():
# If the stack is full, return without adding the element
return
# Increase the rear index by 1 (with wraparound)
self.rear = (self.rear + 1) % self.capacity
# Add the element to the rear position
self.arr[self.rear] = x
# Increase the size of the stack by 1
self.size += 1
def pop(self):
if self.isEmpty():
# If the stack is empty, return without doing anything
return
# Increase the front index by 1 (with wraparound)
self.front = (self.front + 1) % self.capacity
# Decrease the size of the stack by 1
self.size -= 1
def top(self):
if self.isEmpty():
# If the stack is empty, return -1
return -1
# Return the element at the front position
return self.arr[self.front]
def getSize(self):
# Return the current size of the stack
return self.size
# Driver Code
if __name__ == "__main__":
s = Stack(3)
s.push(1)
s.push(2)
s.push(3)
print("current size:", s.getSize())
print(s.top())
s.pop()
print(s.top())
s.pop()
print(s.top())
print("current size:", s.getSize())
using System;
class Stack
{
// Indices to keep track of the front, rear and size of
// the queue
int front, rear, size;
// Maximum capacity of the queue
uint capacity;
// Array used to store the elements
int[] arr;
public Stack(uint capacity)
{
this.capacity = capacity;
// Initially, front index and size are set to 0
front = size = 0;
// Rear index is set to the last index of the array
rear = (int)capacity - 1;
// Allocate memory for the array
arr = new int[capacity];
}
public bool IsFull()
{
// If size is equal to the capacity, the queue is full
return (size == capacity);
}
public bool IsEmpty()
{
// If size is 0, the queue is empty
return (size == 0);
}
public void Push(int x)
{
if (IsFull())
// If the queue is full, return without adding
// the element
return;
// Increase the rear index by 1 (with wraparound)
rear = (rear + 1) % (int)capacity;
// Add the element to the rear position
arr[rear] = x;
// Increase the size of the queue by 1
size++;
}
public void Pop()
{
if (IsEmpty())
return; // If the queue is empty, return without
// doing anything
// Increase the front index by 1 (with wraparound)
front = (front + 1) % (int)capacity;
// Decrease the size of the queue by 1
size--;
}
public int Top()
{
if (IsEmpty())
// If the queue is empty, return -1
return -1;
// Return the element at the front position
return arr[front];
}
public int GetSize()
{
// Return the current size of the queue
return size;
}
}
class Program
{
static void Main(string[] args)
{
// Create a stack of maximum size 3
Stack s = new Stack(3);
s.Push(1);
s.Push(2);
s.Push(3);
Console.WriteLine("current size: " + s.GetSize());
Console.WriteLine(s.Top());
s.Pop();
Console.WriteLine(s.Top());
s.Pop();
Console.WriteLine(s.Top());
Console.WriteLine("current size: " + s.GetSize());
}
}
class Stack {
constructor(capacity) {
// Maximum capacity of the stack
this.capacity = capacity;
// Initially, front index and size are set to 0
this.front = this.size = 0;
// Rear index is set to the last index of the array
this.rear = this.capacity - 1;
// Dynamic allocation of memory for the array
this.arr = new Array(this.capacity);
}
isFull() {
// If size is equal to the capacity, the stack is full
return this.size === this.capacity;
}
isEmpty() {
// If size is 0, the stack is empty
return this.size === 0;
}
push(x) {
if (this.isFull())
// If the stack is full, return without adding the element
return;
// Increase the rear index by 1 (with wraparound)
this.rear = (this.rear + 1) % this.capacity;
// Add the element to the rear position
this.arr[this.rear] = x;
// Increase the size of the stack by 1
this.size++;
}
pop() {
if (this.isEmpty())
// If the stack is empty, return without doing anything
return;
// Increase the front index by 1 (with wraparound)
this.front = (this.front + 1) % this.capacity;
// Decrease the size of the stack by 1
this.size--;
}
top() {
if (this.isEmpty())
// If the stack is empty, return -1
return -1;
// Return the element at the front position
return this.arr[this.front];
}
getSize() {
// Return the current size of the stack
return this.size;
}
}
// Driver code
let s = new Stack(3);
s.push(1);
s.push(2);
s.push(3);
console.log("current size: " + s.getSize());
console.log(s.top());
s.pop();
console.log(s.top());
s.pop();
console.log(s.top());
console.log("current size: " + s.getSize());
Outputcurrent size: 3
1
2
3
current size: 1
References:
Implement Stack using Two Queues
This article was compiled by Sumit Jain and reviewed by the GeeksforGeeks team. Please write comments if you find anything incorrect, or if you want to share more information about the topic discussed above.
Please Login to comment...