Check whether a given graph is Bipartite or not
Last Updated :
20 Oct, 2023
A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
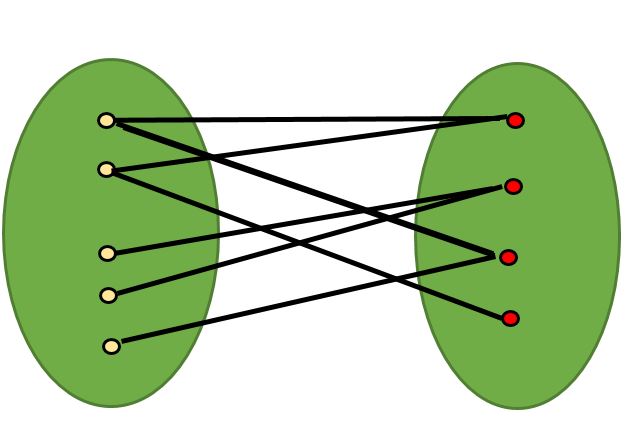
A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color. Note that it is possible to color a cycle graph with even cycle using two colors. For example, see the following graph.
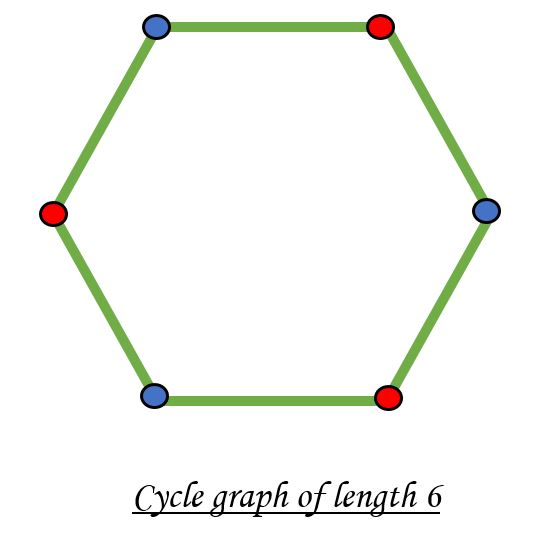
It is not possible to color a cycle graph with odd cycle using two colors.
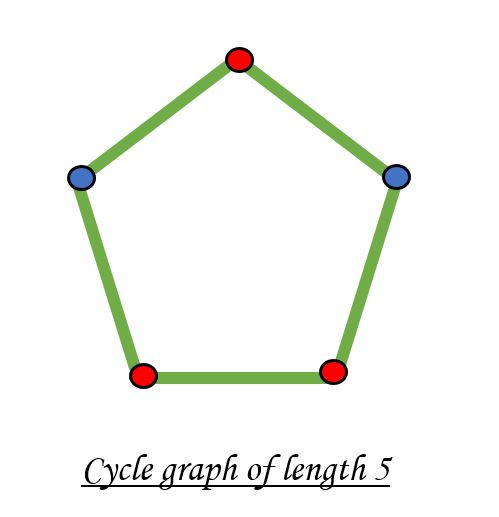
Algorithm to check if a graph is Bipartite:
One approach is to check whether the graph is 2-colorable or not using backtracking algorithm m coloring problem.
Following is a simple algorithm to find out whether a given graph is Bipartite or not using Breadth First Search (BFS).
1. Assign RED color to the source vertex (putting into set U).
2. Color all the neighbors with BLUE color (putting into set V).
3. Color all neighbor’s neighbor with RED color (putting into set U).
4. This way, assign color to all vertices such that it satisfies all the constraints of m way coloring problem where m = 2.
5. While assigning colors, if we find a neighbor which is colored with same color as current vertex, then the graph cannot be colored with 2 vertices (or graph is not Bipartite)
C++
#include <iostream>
#include <queue>
#define V 4
using namespace std;
bool isBipartite(int G[][V], int src)
{
int colorArr[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
queue <int> q;
q.push(src);
while (!q.empty())
{
int u = q.front();
q.pop();
if (G[u][u] == 1)
return false;
for (int v = 0; v < V; ++v)
{
if (G[u][v] && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
int main()
{
int G[][V] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}
};
isBipartite(G, 0) ? cout << "Yes" : cout << "No";
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class Bipartite
{
final static int V = 4;
boolean isBipartite(int G[][],int src)
{
int colorArr[] = new int[V];
for (int i=0; i<V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
LinkedList<Integer>q = new LinkedList<Integer>();
q.add(src);
while (q.size() != 0)
{
int u = q.poll();
if (G[u][u] == 1)
return false;
for (int v=0; v<V; ++v)
{
if (G[u][v]==1 && colorArr[v]==-1)
{
colorArr[v] = 1-colorArr[u];
q.add(v);
}
else if (G[u][v]==1 && colorArr[v]==colorArr[u])
return false;
}
}
return true;
}
public static void main (String[] args)
{
int G[][] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}
};
Bipartite b = new Bipartite();
if (b.isBipartite(G, 0))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
class Graph():
def __init__(self, V):
self.V = V
self.graph = [[0 for column in range(V)] \
for row in range(V)]
def isBipartite(self, src):
colorArr = [-1] * self.V
colorArr[src] = 1
queue = []
queue.append(src)
while queue:
u = queue.pop()
if self.graph[u][u] == 1:
return False;
for v in range(self.V):
if self.graph[u][v] == 1 and colorArr[v] == -1:
colorArr[v] = 1 - colorArr[u]
queue.append(v)
elif self.graph[u][v] == 1 and colorArr[v] == colorArr[u]:
return False
return True
g = Graph(4)
g.graph = [[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]
]
print ("Yes" if g.isBipartite(0) else "No")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
readonly static int V = 4;
bool isBipartite(int [,]G, int src)
{
int []colorArr = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
List<int>q = new List<int>();
q.Add(src);
while (q.Count != 0)
{
int u = q[0];
q.RemoveAt(0);
if (G[u, u] == 1)
return false;
for (int v = 0; v < V; ++v)
{
if (G[u, v] == 1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.Add(v);
}
else if (G[u, v] == 1 &&
colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
public static void Main(String[] args)
{
int [,]G = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}};
GFG b = new GFG();
if (b.isBipartite(G, 0))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
let V = 4;
function isBipartite(G,src)
{
let colorArr = new Array(V);
for (let i=0; i<V; ++i)
colorArr[i] = -1;
colorArr[src] = 1;
let q = [];
q.push(src);
while (q.length != 0)
{
let u = q.shift();
if (G[u][u] == 1)
return false;
for (let v=0; v<V; ++v)
{
if (G[u][v]==1 && colorArr[v]==-1)
{
colorArr[v] = 1-colorArr[u];
q.push(v);
}
else if (G[u][v]==1 && colorArr[v]==colorArr[u])
return false;
}
}
return true;
}
let G=[[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]];
if (isBipartite(G, 0))
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity : O(V*V) as adjacency matrix is used for graph but can be made O(V+E) by using adjacency list
Auxiliary Space: O(V) due to queue and color vector.
The above algorithm works only if the graph is connected. In above code, we always start with source 0 and assume that vertices are visited from it. One important observation is a graph with no edges is also Bipartite. Note that the Bipartite condition says all edges should be from one set to another.
We can extend the above code to handle cases when a graph is not connected. The idea is repeatedly called above method for all not yet visited vertices.
C++
#include <bits/stdc++.h>
using namespace std;
const int V = 4;
bool isBipartiteUtil(int G[][V], int src, int colorArr[])
{
colorArr[src] = 1;
queue<int> q;
q.push(src);
while (!q.empty()) {
int u = q.front();
q.pop();
if (G[u][u] == 1)
return false;
for (int v = 0; v < V; ++v) {
if (G[u][v] && colorArr[v] == -1) {
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] && colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
bool isBipartite(int G[][V])
{
int colorArr[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr) == false)
return false;
return true;
}
int main()
{
int G[][V] = { { 0, 1, 0, 1 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 } };
isBipartite(G) ? cout << "Yes" : cout << "No";
return 0;
}
|
Java
import java.util.*;
class Bipartite {
public static int V = 4;
public static boolean
isBipartiteUtil(int G[][], int src, int colorArr[])
{
colorArr[src] = 1;
LinkedList<Integer> q = new LinkedList<Integer>();
q.add(src);
while (!q.isEmpty()) {
int u = q.getFirst();
q.pop();
if (G[u][u] == 1)
return false;
for (int v = 0; v < V; ++v) {
if (G[u][v] == 1 && colorArr[v] == -1) {
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u][v] == 1
&& colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
public static boolean isBipartite(int G[][])
{
int colorArr[] = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr)
== false)
return false;
return true;
}
public static void main(String[] args)
{
int G[][] = { { 0, 1, 0, 1 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 } };
if (isBipartite(G))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
class Graph():
def __init__(self, V):
self.V = V
self.graph = [[0 for column in range(V)]
for row in range(V)]
self.colorArr = [-1 for i in range(self.V)]
def isBipartiteUtil(self, src):
queue = []
queue.append(src)
while queue:
u = queue.pop()
if self.graph[u][u] == 1:
return False
for v in range(self.V):
if (self.graph[u][v] == 1 and
self.colorArr[v] == -1):
self.colorArr[v] = 1 - self.colorArr[u]
queue.append(v)
elif (self.graph[u][v] == 1 and
self.colorArr[v] == self.colorArr[u]):
return False
return True
def isBipartite(self):
self.colorArr = [-1 for i in range(self.V)]
for i in range(self.V):
if self.colorArr[i] == -1:
if not self.isBipartiteUtil(i):
return False
return True
g = Graph(4)
g.graph = [[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]]
print ("Yes" if g.isBipartite() else "No")
|
C#
using System;
using System.Collections.Generic;
class GFG {
public static int V = 4;
public static bool isBipartiteUtil(int[, ] G, int src,
int[] colorArr)
{
colorArr[src] = 1;
Queue<int> q = new Queue<int>();
q.Enqueue(src);
while (q.Count != 0) {
int u = q.Peek();
q.Dequeue();
if (G[u, u] == 1)
return false;
for (int v = 0; v < V; ++v) {
if (G[u, v] == 1 && colorArr[v] == -1) {
colorArr[v] = 1 - colorArr[u];
q.Enqueue(v);
}
else if (G[u, v] == 1
&& colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
public static bool isBipartite(int[, ] G)
{
int[] colorArr = new int[V];
for (int i = 0; i < V; ++i)
colorArr[i] = -1;
for (int i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr)
== false)
return false;
return true;
}
public static void Main(String[] args)
{
int[, ] G = { { 0, 1, 0, 1 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 } };
if (isBipartite(G))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
var V = 4;
function isBipartiteUtil(G, src, colorArr)
{
colorArr[src] = 1;
var q = [];
q.push(src);
while (q.length != 0)
{
var u = q[0];
q.shift();
if (G[u, u] == 1)
return false;
for (var v = 0; v < V; ++v)
{
if (G[u][v] == 1 && colorArr[v] == -1)
{
colorArr[v] = 1 - colorArr[u];
q.push(v);
}
else if (G[u, v] == 1
&& colorArr[v] == colorArr[u])
return false;
}
}
return true;
}
function isBipartite(G)
{
var colorArr = Array(V);
for (var i = 0; i < V; ++i)
colorArr[i] = -1;
for (var i = 0; i < V; i++)
if (colorArr[i] == -1)
if (isBipartiteUtil(G, i, colorArr)
== false)
return false;
return true;
}
var G = [ [ 0, 1, 0, 1 ],
[ 1, 0, 1, 0 ],
[ 0, 1, 0, 1 ],
[ 1, 0, 1, 0 ] ];
if (isBipartite(G))
document.write("Yes");
else
document.write("No");
</script>
|
Time complexity: O(V*V).
Auxiliary Space: O(V), because we have a V-size array.
If Graph is represented using Adjacency List .Time Complexity will be O(V+E).
Works for connected as well as disconnected graph.
C++
#include <bits/stdc++.h>
using namespace std;
bool isBipartite(int V, vector<int> adj[])
{
vector<int> col(V, -1);
queue<pair<int, int> > q;
for (int i = 0; i < V; i++) {
if (col[i] == -1) {
q.push({ i, 0 });
col[i] = 0;
while (!q.empty()) {
pair<int, int> p = q.front();
q.pop();
int v = p.first;
int c = p.second;
for (int j : adj[v]) {
if (col[j] == c)
return 0;
if (col[j] == -1) {
col[j] = (c) ? 0 : 1;
q.push({ j, col[j] });
}
}
}
}
}
return 1;
}
int main()
{
int V, E;
V = 4 , E = 8;
vector<int> adj[V];
adj[0] = {1,3};
adj[1] = {0,2};
adj[2] = {1,3};
adj[3] = {0,2};
bool ans = isBipartite(V, adj);
if (ans)
cout << "Yes\n";
else
cout << "No\n";
return 0;
}
|
Java
import java.util.*;
public class GFG{
static class Pair{
int first, second;
Pair(int f, int s){
first = f;
second = s;
}
}
static boolean isBipartite(int V, ArrayList<ArrayList<Integer>> adj)
{
int col[] = new int[V];
Arrays.fill(col, -1);
Queue<Pair> q = new LinkedList<Pair>();
for (int i = 0; i < V; i++) {
if (col[i] == -1) {
q.add(new Pair(i, 0));
col[i] = 0;
while (!q.isEmpty()) {
Pair p = q.peek();
q.poll();
int v = p.first;
int c = p.second;
for (int j : adj.get(v))
{
if (col[j] == c)
return false;
if (col[j] == -1)
{
col[j] = (c==1) ? 0 : 1;
q.add(new Pair(j, col[j]));
}
}
}
}
}
return true;
}
public static void main(String args[])
{
int V, E;
V = 4 ;
E = 8;
ArrayList<ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>();
for(int i = 0; i < V; i++){
adj.add(new ArrayList<Integer>());
}
adj.get(0).add(1);
adj.get(0).add(3);
adj.get(1).add(0);
adj.get(1).add(2);
adj.get(2).add(1);
adj.get(2).add(3);
adj.get(3).add(0);
adj.get(3).add(2);
boolean ans = isBipartite(V, adj);
if (ans)
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def isBipartite(V, adj):
col = [-1]*(V)
q = []
for i in range(V):
if (col[i] == -1):
q.append([i, 0])
col[i] = 0
while len(q) != 0:
p = q[0]
q.pop(0)
v = p[0]
c = p[1]
for j in adj[v]:
if (col[j] == c):
return False
if (col[j] == -1):
if c == 1:
col[j] = 0
else:
col[j] = 1
q.append([j, col[j]])
return True
V, E = 4, 8
adj = []
adj.append([1,3])
adj.append([0,2])
adj.append([1,3])
adj.append([0,2])
ans = isBipartite(V, adj)
if (ans):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG {
static bool isBipartite(int V, List<List<int>> adj)
{
int[] col = new int[V];
Array.Fill(col, -1);
List<Tuple<int,int>> q = new List<Tuple<int,int>>();
for (int i = 0; i < V; i++) {
if (col[i] == -1) {
q.Add(new Tuple<int,int>(i, 0));
col[i] = 0;
while (q.Count > 0) {
Tuple<int,int> p = q[0];
q.RemoveAt(0);
int v = p.Item1;
int c = p.Item2;
foreach(int j in adj[v])
{
if (col[j] == c)
return false;
if (col[j] == -1)
{
col[j] = (c==1) ? 0 : 1;
q.Add(new Tuple<int,int>(j, col[j]));
}
}
}
}
}
return true;
}
static void Main() {
int V;
V = 4 ;
List<List<int>> adj = new List<List<int>>();
for(int i = 0; i < V; i++){
adj.Add(new List<int>());
}
adj[0].Add(1);
adj[0].Add(3);
adj[1].Add(0);
adj[1].Add(2);
adj[2].Add(1);
adj[2].Add(3);
adj[3].Add(0);
adj[3].Add(2);
bool ans = isBipartite(V, adj);
if (ans)
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
class Pair
{
constructor(f,s)
{
this.first = f;
this.second = s;
}
}
function isBipartite(V, adj)
{
let col = new Array(V);
for(let i = 0; i < V; i++)
col[i] = -1;
let q = [];
for (let i = 0; i < V; i++) {
if (col[i] == -1) {
q.push(new Pair(i, 0));
col[i] = 0;
while (q.length!=0) {
let p = q[0];
q.shift();
let v = p.first;
let c = p.second;
for (let j of adj[v])
{
if (col[j] == c)
return false;
if (col[j] == -1)
{
col[j] = (c==1) ? 0 : 1;
q.push(new Pair(j, col[j]));
}
}
}
}
}
return true;
}
let V, E;
V = 4 ;
E = 8;
let adj = [];
for(let i = 0; i < V; i++){
adj.push([]);
}
adj[0].push(1);
adj[0].push(3);
adj[1].push(0);
adj[1].push(2);
adj[2].push(1);
adj[2].push(3);
adj[3].push(0);
adj[3].push(2);
let ans = isBipartite(V, adj);
if (ans)
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(V+E)
Auxiliary Space: O(V)
Exercise:
1. Can DFS algorithm be used to check the bipartite-ness of a graph? If yes, how?
Explanation:
The algorithm can be described as follows:
Step 1: To perform a DFS traversal, we require a starting node and an array to track visited nodes.
However, instead of using a visited array, we will utilize a color array where each node is initially
assigned the value -1 to indicate that it has not been colored yet.
Step 2: In the DFS function call, it is important to pass the assigned color value and store it in the color array.
We will attempt to color the nodes using 0 and 1, although alternative colors can also be chosen.
Starting with color 0 is suggested, but starting with color 1 is also acceptable; the key is to ensure that adjacent nodes
have the opposite color to their current node.
Step 3: During the DFS traversal, we explore uncolored neighbors by utilizing the adjacency list.
For each uncolored node encountered, we assign it the opposite color of its current node.
Step 4: If, at any point, we encounter an adjacent node in the adjacency list that has already been colored and shares
the same color as the current node, it implies that coloring is not possible.
Consequently, we return false, indicating that the given graph is not bipartite. Otherwise, we continue returning true.
Solution :
C++
#include <iostream>
using namespace std;
#define V 4
bool colorGraph(int G[][V],int color[],int pos, int c){
if(color[pos] != -1 && color[pos] !=c)
return false;
color[pos] = c;
bool ans = true;
for(int i=0;i<V;i++){
if(G[pos][i]){
if(color[i] == -1)
ans &= colorGraph(G,color,i,1-c);
if(color[i] !=-1 && color[i] != 1-c)
return false;
}
if (!ans)
return false;
}
return true;
}
bool isBipartite(int G[][V]){
int color[V];
for(int i=0;i<V;i++)
color[i] = -1;
int pos = 0;
return colorGraph(G,color,pos,1);
}
int main()
{
int G[][V] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}
};
isBipartite(G) ? cout<< "Yes" : cout << "No";
return 0;
}
|
Java
class GFG
{
static final int V = 4;
static boolean colorGraph(int G[][],
int color[],
int pos, int c)
{
if (color[pos] != -1 &&
color[pos] != c)
return false;
color[pos] = c;
boolean ans = true;
for (int i = 0; i < V; i++)
{
if (G[pos][i] == 1)
{
if (color[i] == -1)
ans &= colorGraph(G, color, i, 1 - c);
if (color[i] != -1 && color[i] != 1 - c)
return false;
}
if (!ans)
return false;
}
return true;
}
static boolean isBipartite(int G[][])
{
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = -1;
int pos = 0;
return colorGraph(G, color, pos, 1);
}
public static void main(String[] args)
{
int G[][] = { { 0, 1, 0, 1 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 } };
if (isBipartite(G))
System.out.print("Yes");
else
System.out.print("No");
}
}
|
Python3
V = 4
def colorGraph(G, color, pos, c):
if color[pos] != -1 and color[pos] != c:
return False
color[pos] = c
ans = True
for i in range(0, V):
if G[pos][i]:
if color[i] == -1:
ans &= colorGraph(G, color, i, 1-c)
if color[i] !=-1 and color[i] != 1-c:
return False
if not ans:
return False
return True
def isBipartite(G):
color = [-1] * V
pos = 0
return colorGraph(G, color, pos, 1)
if __name__ == "__main__":
G = [[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]]
if isBipartite(G): print("Yes")
else: print("No")
|
C#
using System;
class GFG
{
static readonly int V = 4;
static bool colorGraph(int [,]G,
int []color,
int pos, int c)
{
if (color[pos] != -1 &&
color[pos] != c)
return false;
color[pos] = c;
bool ans = true;
for (int i = 0; i < V; i++)
{
if (G[pos, i] == 1)
{
if (color[i] == -1)
ans &= colorGraph(G, color, i, 1 - c);
if (color[i] != -1 && color[i] != 1 - c)
return false;
}
if (!ans)
return false;
}
return true;
}
static bool isBipartite(int [,]G)
{
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = -1;
int pos = 0;
return colorGraph(G, color, pos, 1);
}
public static void Main(String[] args)
{
int [,]G = {{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 },
{ 0, 1, 0, 1 },
{ 1, 0, 1, 0 }};
if (isBipartite(G))
Console.Write("Yes");
else
Console.Write("No");
}
}
|
Javascript
<script>
var V = 4;
function colorGraph(G, color, pos, c) {
if (color[pos] != -1 && color[pos] != c) return false;
color[pos] = c;
var ans = true;
for (var i = 0; i < V; i++) {
if (G[pos][i] == 1) {
if (color[i] == -1) ans &= colorGraph(G, color, i, 1 - c);
if (color[i] != -1 && color[i] != 1 - c) return false;
}
if (!ans) return false;
}
return true;
}
function isBipartite(G) {
var color = new Array(V).fill(0);
for (var i = 0; i < V; i++) color[i] = -1;
var pos = 0;
return colorGraph(G, color, pos, 1);
}
var G = [
[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0],
];
if (isBipartite(G)) document.write("Yes");
else document.write("No");
</script>
|
Time Complexity: O(V+E)
Auxiliary Space: O(V)
References:
http://en.wikipedia.org/wiki/Graph_coloring
http://en.wikipedia.org/wiki/Bipartite_graph
This article is compiled by Aashish Barnwal.
Please Login to comment...