Open In App

Minimum steps to reach target by a Knight | Set 1

Last Updated : 09 May, 2024
Improve
Improve
Like Article
Like
Save
Share
Report

Given a square chessboard of N x N size, the position of the Knight and the position of a target are given. We need to find out the minimum steps a Knight will take to reach the target position.

Examples: 

Input: 

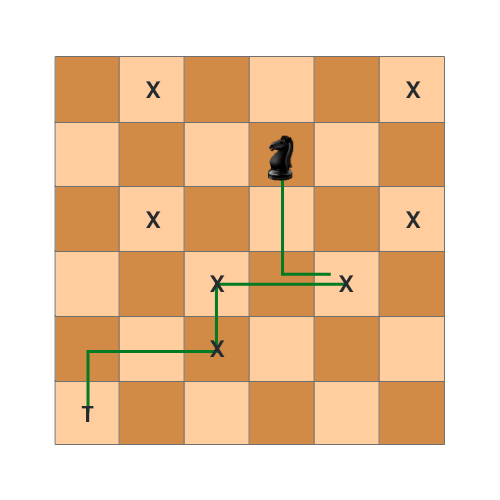
kNIGHT

Knight

knightPosition: (1, 3) , targetPosition: (5, 0)

Output: 3
Explanation: In above diagram Knight takes 3 step to reach 
                      from (1, 3) to (5, 0) 
                     (1, 3) -> (3, 4) -> (4, 2) -> (5, 0)  

Recommended Practice
Steps by Knight
Try It!

Minimum steps to reach the target by a Knight using BFS:

To solve the problem follow the below idea:

This problem can be seen as the shortest path in an unweighted graph. Therefore, BFS is an appropriate algorithm to solve this problem. 

Try all 8 possible positions where a Knight can reach from its position. If the reachable position is not already visited and is inside the board, push this state into the queue with a distance 1 more than its parent state. During the BFS traversal, if the current position is target position then return the distance of the target position.

Below is the implementation of the above approach:

C++ 
#include <bits/stdc++.h>
using namespace std;

// structure for storing a cell's data
struct cell {
    int x, y;
    int dis;
    cell() {}
    cell(int x, int y, int dis)
        : x(x)
        , y(y)
        , dis(dis)
    {
    }
};

// Utility method returns true if (x, y) lies
// inside Board
bool isInside(int x, int y, int N)
{
    if (x >= 1 && x <= N && y >= 1 && y <= N)
        return true;
    return false;
}

// Method returns minimum step
// to reach target position
int minStepToReachTarget(int knightPos[], int targetPos[],
                         int N)
{
    // x and y direction, where a knight can move
    int dx[] = { -2, -1, 1, 2, -2, -1, 1, 2 };
    int dy[] = { -1, -2, -2, -1, 1, 2, 2, 1 };

    // queue for storing states of knight in board
    queue<cell> q;

    // push starting position of knight with 0 distance
    q.push(cell(knightPos[0], knightPos[1], 0));

    cell t;
    int x, y;
    bool visit[N + 1][N + 1];

    // make all cell unvisited
    memset(visit, false, sizeof(visit));

    // visit starting state
    visit[knightPos[0]][knightPos[1]] = true;

    // loop until we have one element in queue
    while (!q.empty()) {
        t = q.front();
        q.pop();

        // if current cell is equal to target cell,
        // return its distance
        if (t.x == targetPos[0] && t.y == targetPos[1])
            return t.dis;

        // loop for all reachable states
        for (int i = 0; i < 8; i++) {
            x = t.x + dx[i];
            y = t.y + dy[i];

            // If reachable state is not yet visited and
            // inside board, push that state into queue
            if (isInside(x, y, N) && !visit[x][y]) {
                visit[x][y] = true;
                q.push(cell(x, y, t.dis + 1));
            }
        }
    }

    // If no valid path found, return -1
    return -1;
}

// Driver code
int main()
{
    int N = 30;
    int knightPos[] = { 1, 1 };
    int targetPos[] = { 30, 30 };

    // Function call
    cout << minStepToReachTarget(knightPos, targetPos, N);
    return 0;
}
Java 
// Java program to find minimum steps to reach to
// specific cell in minimum moves by Knight

import java.io.*;
import java.util.*;

// Java program to find minimum steps to reach to
// specific cell in minimum moves by Knight
public class GFG {

    // Class for storing a cell's data
    static class cell {
        int x, y;
        int dis;

        public cell(int x, int y, int dis)
        {
            this.x = x;
            this.y = y;
            this.dis = dis;
        }
    }

    // Utility method returns true if (x, y) lies
    // inside Board
    static boolean isInside(int x, int y, int N)
    {
        if (x >= 1 && x <= N && y >= 1 && y <= N)
            return true;
        return false;
    }

    // Method returns minimum step
    // to reach target position
    static int minStepToReachTarget(int knightPos[],
                                    int targetPos[], int N)
    {
        // x and y direction, where a knight can move
        int dx[] = { -2, -1, 1, 2, -2, -1, 1, 2 };
        int dy[] = { -1, -2, -2, -1, 1, 2, 2, 1 };

        // queue for storing states of knight in board
        Queue<cell> q = new LinkedList<>();

        // push starting position of knight with 0 distance
        q.add(new cell(knightPos[0], knightPos[1], 0));

        cell t;
        int x, y;
        boolean visit[][] = new boolean
            [N + 1][N + 1]; // default initialized to false

        // visit starting state
        visit[knightPos[0]][knightPos[1]] = true;

        // loop until we have one element in queue
        while (!q.isEmpty()) {
            t = q.poll();

            // if current cell is equal to target cell,
            // return its distance
            if (t.x == targetPos[0] && t.y == targetPos[1])
                return t.dis;

            // loop for all reachable states
            for (int i = 0; i < 8; i++) {
                x = t.x + dx[i];
                y = t.y + dy[i];

                // If reachable state is not yet visited and
                // inside board, push that state into queue
                if (isInside(x, y, N) && !visit[x][y]) {
                    visit[x][y] = true;
                    q.add(new cell(x, y, t.dis + 1));
                }
            }
        }
        return Integer.MAX_VALUE;
    }

    // Driver code
    public static void main(String[] args)
    {
        int N = 30;
        int knightPos[] = { 1, 1 };
        int targetPos[] = { 30, 30 };

        // Function call
        System.out.println(
            minStepToReachTarget(knightPos, targetPos, N));
    }
}

// This code contributed by Rajput-Ji
Python 
# Python3 code to find minimum steps to reach
# to specific cell in minimum moves by Knight


class cell:

    def __init__(self, x=0, y=0, dist=0):
        self.x = x
        self.y = y
        self.dist = dist

# checks whether given position is
# inside the board


def isInside(x, y, N):
    if (x >= 1 and x <= N and
            y >= 1 and y <= N):
        return True
    return False

# Method returns minimum step to reach
# target position


def minStepToReachTarget(knightpos,
                         targetpos, N):

    # all possible movements for the knight
    dx = [2, 2, -2, -2, 1, 1, -1, -1]
    dy = [1, -1, 1, -1, 2, -2, 2, -2]

    queue = []

    # push starting position of knight
    # with 0 distance
    queue.append(cell(knightpos[0], knightpos[1], 0))

    # make all cell unvisited
    visited = [[False for i in range(N + 1)]
               for j in range(N + 1)]

    # visit starting state
    visited[knightpos[0]][knightpos[1]] = True

    # loop until we have one element in queue
    while(len(queue) > 0):

        t = queue[0]
        queue.pop(0)

        # if current cell is equal to target
        # cell, return its distance
        if(t.x == targetpos[0] and
           t.y == targetpos[1]):
            return t.dist

        # iterate for all reachable states
        for i in range(8):

            x = t.x + dx[i]
            y = t.y + dy[i]

            if(isInside(x, y, N) and not visited[x][y]):
                visited[x][y] = True
                queue.append(cell(x, y, t.dist + 1))


# Driver Code
if __name__ == '__main__':
    N = 30
    knightpos = [1, 1]
    targetpos = [30, 30]

    # Function call
    print(minStepToReachTarget(knightpos,
                               targetpos, N))

# This code is contributed by
# Kaustav kumar Chanda
C# 
// C# program to find minimum steps to reach to
// specific cell in minimum moves by Knight

using System;
using System.Collections.Generic;

class GFG {

    // Class for storing a cell's data
    public class cell {
        public int x, y;
        public int dis;

        public cell(int x, int y, int dis)
        {
            this.x = x;
            this.y = y;
            this.dis = dis;
        }
    }

    // Utility method returns true
    // if (x, y) lies inside Board
    static bool isInside(int x, int y, int N)
    {
        if (x >= 1 && x <= N && y >= 1 && y <= N)
            return true;
        return false;
    }

    // Method returns minimum step
    // to reach target position
    static int minStepToReachTarget(int[] knightPos,
                                    int[] targetPos, int N)
    {
        // x and y direction, where a knight can move
        int[] dx = { -2, -1, 1, 2, -2, -1, 1, 2 };
        int[] dy = { -1, -2, -2, -1, 1, 2, 2, 1 };

        // queue for storing states of knight in board
        Queue<cell> q = new Queue<cell>();

        // push starting position of knight with 0 distance
        q.Enqueue(new cell(knightPos[0], knightPos[1], 0));

        cell t;
        int x, y;
        bool[, ] visit = new bool[N + 1, N + 1];

        // make all cell unvisited
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++)
                visit[i, j] = false;

        // visit starting state
        visit[knightPos[0], knightPos[1]] = true;

        // loop until we have one element in queue
        while (q.Count != 0) {
            t = q.Peek();
            q.Dequeue();

            // if current cell is equal to target cell,
            // return its distance
            if (t.x == targetPos[0] && t.y == targetPos[1])
                return t.dis;

            // loop for all reachable states
            for (int i = 0; i < 8; i++) {
                x = t.x + dx[i];
                y = t.y + dy[i];

                // If reachable state is not yet visited and
                // inside board, push that state into queue
                if (isInside(x, y, N) && !visit[x, y]) {
                    visit[x, y] = true;
                    q.Enqueue(new cell(x, y, t.dis + 1));
                }
            }
        }
        return int.MaxValue;
    }

    // Driver code
    public static void Main(String[] args)
    {
        int N = 30;
        int[] knightPos = { 1, 1 };
        int[] targetPos = { 30, 30 };

        // Function call
        Console.WriteLine(
            minStepToReachTarget(knightPos, targetPos, N));
    }
}
// This code is contributed by 29AjayKumar
Javascript 
<script>
// Javascript program to find minimum steps to reach to
// specific cell in minimum moves by Knight

// Class for storing a cell's data
class cell
{
    constructor(x,y,dis)
    {
        this.x = x;
            this.y = y;
            this.dis = dis;
    }
}

// Utility method returns true if (x, y) lies
    // inside Board
function isInside(x,y,N)
{
    if (x >= 1 && x <= N && y >= 1 && y <= N)
            return true;
        return false;
}

// Method returns minimum step
    // to reach target position
function minStepToReachTarget(knightPos,targetPos,N)
{
    // x and y direction, where a knight can move
        let dx = [ -2, -1, 1, 2, -2, -1, 1, 2 ];
        let dy = [ -1, -2, -2, -1, 1, 2, 2, 1 ];
  
        // queue for storing states of knight in board
        let q = [];
  
        // push starting position of knight with 0 distance
        q.push(new cell(knightPos[0], knightPos[1], 0));
  
        let t;
        let x, y;
        let visit = new Array(N + 1);
  
        // make all cell unvisited
        for (let i = 1; i <= N; i++)
        {
            visit[i]=new Array(N+1);
            for (let j = 1; j <= N; j++)
                visit[i][j] = false;
        }
  
        // visit starting state
        visit[knightPos[0]][knightPos[1]] = true;
  
        // loop until we have one element in queue
        while (q.length!=0) {
            t = q.shift();
            
  
            // if current cell is equal to target cell,
            // return its distance
            if (t.x == targetPos[0] && t.y == targetPos[1])
                return t.dis;
  
            // loop for all reachable states
            for (let i = 0; i < 8; i++) {
                x = t.x + dx[i];
                y = t.y + dy[i];
  
                // If reachable state is not yet visited and
                // inside board, push that state into queue
                if (isInside(x, y, N) && !visit[x][y]) {
                    visit[x][y] = true;
                    q.push(new cell(x, y, t.dis + 1));
                }
            }
        }
        return Number.MAX_VALUE;
}

// Driver code
let N = 30;
let knightPos=[1,1];
let targetPos=[30,30];
document.write(
            minStepToReachTarget(
                knightPos, targetPos, N));


// This code is contributed by rag2127
</script>

Output
20

Time complexity: O(N2). In the worst case, all the cells will be visited
Auxiliary Space: O(N2). The nodes are stored in a queue. 




U

Utkarsh Trivedi
Improve
Previous Article
Hamiltonian Cycle
Next Article
Search a Word in a 2D Grid of characters (Word Search)

Similar Reads

Minimum steps to reach target by a Knight | Set 2
Given a square chessboard of N x N size, the position of Knight and position of a target is given, the task is to find out the minimum steps a Knight will take to reach the target position. Examples : Input : (2, 4) - knight's position, (6, 4) - target cell Output : 2 Input : (4, 5) (1, 1) Output : 3 A BFS approach to solve the above problem has al
15+ min read
Count of all possible ways to reach a target by a Knight
Given two integers N, M denoting N×M chessboard, the task is to count the number of ways a knight can reach (N, M) starting from (0, 0). Since the answer can be very large, print the answer modulo 109+7. Example: Input: N =3, M= 3Output: 2Explanation: Two ways to reach (3, 3) form (0, 0) are as follows:(0, 0) ? (1, 2) ? (3, 3)(0, 0) ? (2, 1) ? (3,
10 min read
Minimum Steps to Reach the Target
Given an array arr[] of size N and two integer values target and K, the task is to find the minimum number of steps required to reach the target element starting from index 0. In one step, you can either: Move from the current index i to index j if arr[i] is equal to arr[j] and i != j.Move to (i + k) or (i – k).Note: It is not allowed to move outsi
13 min read
Puzzle | Can a Knight reach bottom from top by visiting all squares
Puzzle Is there a way for a chess knight to start at the top-left corner from a N x N chessboard, visit all the squares of the board exactly once and end at the lower-right corner. Solution We need to traverse all the squares of the chessboard exactly once. Also, the moves of the knight are L-shaped, that is, traverse two squares vertically or hori
2 min read
All possible points where knight can reach in one move
Given an integer N and knight position {x, y}, the task is to print all possible sets of points that the knight can reach in one move on an N*N chessboard. Note: Output the points in sorted order. Examples: Input: N = 4, x = 2, y = 2Output:(0, 1)(0, 3)(1, 0)(3, 0)Explanation: Knight can be moved from (2, 2) to (0, 1), (0, 3), (1, 0) and (3, 0). Inp
7 min read
Minimum moves to reach target on a infinite line | Set 2
Given a target position on the infinite number line, (-infinity to +infinity). Starting form 0 you have to reach the target by moving as described: In ith move, you can take i steps forward or backward. Find the minimum number of moves required to reach the target. Examples : Input : target = 3 Output : 2 Explanation: On the first move we step from
6 min read
Minimum number of sum and modulo operations using given numbers to reach target
Given a number N, an array arr[], and a target number K, the task is to find minimum number of moves to reach K by choosing any array element and changing N to (N + arr[i]) mod 100000 in each move. Examples: Input: N = 99880, K = 89, arr = {100, 3}Output: 5Explanation: Number "100" is used 2 times and the number "3" is pushed 3 times, resulting in
6 min read
Minimum swaps such that at least K points reach target within T time
Given N points moving along the X axis to the right whose initial position and speed are given in two arrays X[] (sorted in increasing order) and V[]. If at any time a point with a higher speed reaches a slow moving point then they will both continue moving with the slower speed. The task is to find out the minimum number of swaps we can perform on
7 min read
Find minimum moves to reach target on an infinite line
Given a target position on infinite number line, i.e -infinity to +infinity. Starting form 0 you have to reach the target by moving as described : In ith move you can take i steps forward or backward. Find the minimum number of moves require to reach the target. Examples: Input : target = 3 Output : 2 Explanation: On the first move we step from 0 t
7 min read
Minimum steps to reach any of the boundary edges of a matrix | Set-2
Given an N X M matrix, where ai, j = 1 denotes the cell is not empty, ai, j = 0 denotes the cell is empty and ai, j = 2, denotes that you are standing at that cell. You can move vertically up or down and horizontally left or right to any cell which is empty. The task is to find the minimum number of steps to reach any boundary edge of the matrix. P
14 min read
Article Tags :
Practice Tags :
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox