Find the first circular tour that visits all petrol pumps
Last Updated :
19 Apr, 2024
Given information about N petrol pumps (say arr[]) that are present in a circular path. The information consists of the distance of the next petrol pump from the current one (in arr[i][1]) and the amount of petrol stored in that petrol pump (in arr[i][0]). Consider a truck with infinite capacity that consumes 1 unit of petrol to travel 1 unit distance. The task is to find the index of the first starting point such that the truck can visit all the petrol pumps and come back to that starting point.
Note: Return -1 if no such tour exists.
Examples:
Input: arr[] = {{4, 6}, {6, 5}, {7, 3}, {4, 5}}.
Output: 1
Explanation: If started from 1st index then a circular tour can be covered.
Input: arr[] {{6, 4}, {3, 6}, {7, 3}}
Output: 2
Naive Approach:
As the capacity of the truck is infinite it is feasible to fill the truck with all the amount of petrol available at each petrol pump.
A Simple Solution is to consider every petrol pumps as a starting point and see if there is a possible tour. If we find a starting point with a feasible solution, we return that starting point.
Time Complexity: O(N2)
Auxiliary Space: O(1)
First Circular Tour Using Queue:
Instead of checking the whole array for each starting point, we can store the current tour inside a queue.
At the moment, the current amount of petrol becomes inefficient (i.e., negative) to reach the next petrol pump, remove the current starting point from the queue and consider the next point as the new starting point.
Instead of building a separate queue, we can use the array itself as a queue with the help of start and end pointers.
Note: Each petrol pump will be added in the queue at most twice and will be removed at most once.
Illustration:
Below image is a dry run of the above approach:
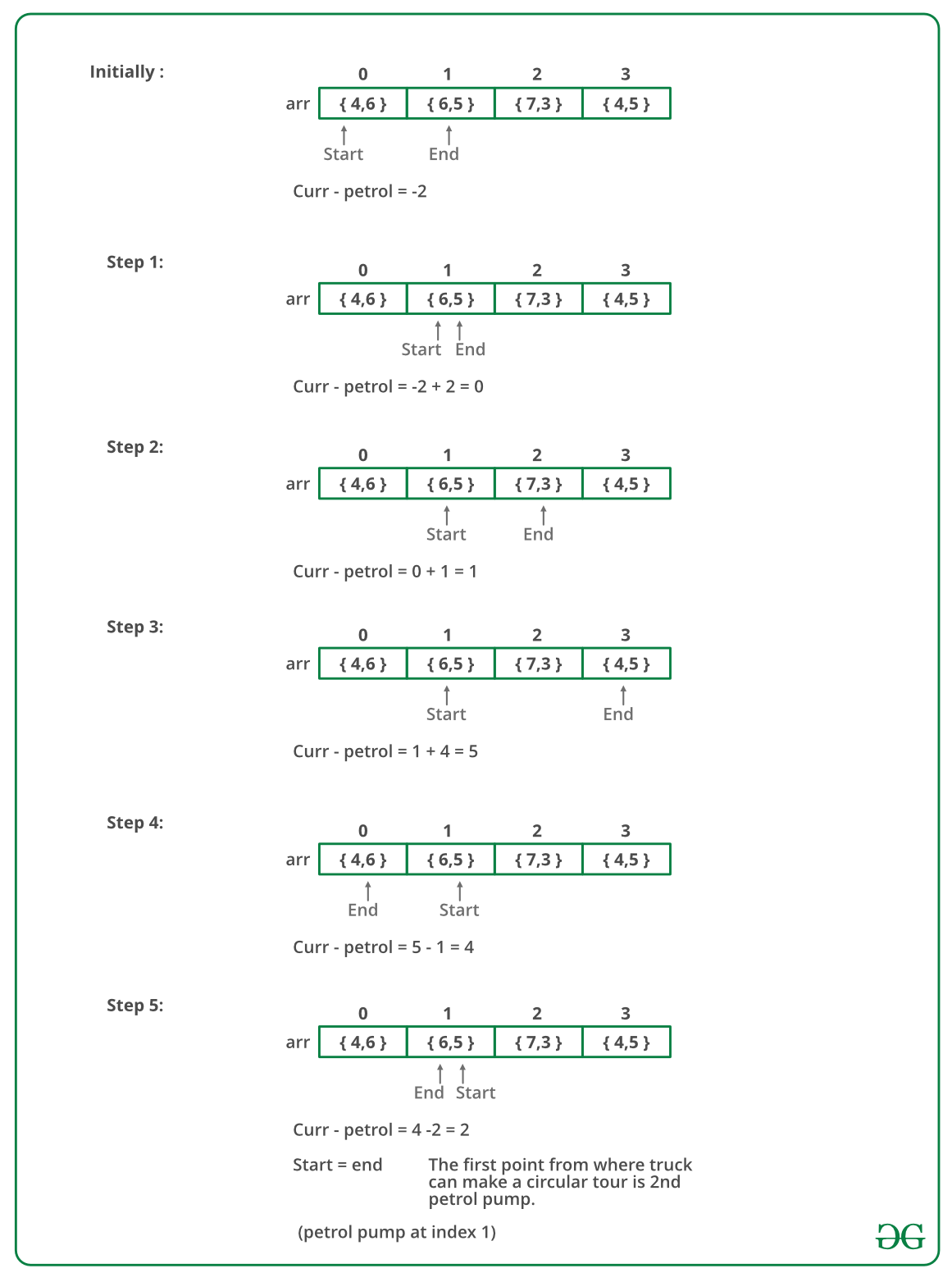
Follow the below steps to implement the idea:
- Set two pointers, start = 0 and end = 1 to use the array as a queue.
- If the amount of petrol is efficient to reach the next petrol pump then increment the end pointer (circularly).
- Otherwise, remove the starting point of the current tour, i.e., increment the start pointer.
- If the start pointer reaches N then such a tour is not possible. Otherwise, return the starting point of the tour.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump
{
public:
int petrol;
int distance;
};
int printTour(petrolPump arr[], int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1) % n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1) % n;
}
return start;
}
int main()
{
petrolPump arr[] = {{6, 4}, {3, 6}, {7, 3}};
int n = sizeof(arr)/sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1)? cout<<"No solution": cout<<"Start = "<<start;
return 0;
}
|
C
#include <stdio.h>
struct petrolPump
{
int petrol;
int distance;
};
int printTour(struct petrolPump arr[], int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1)%n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1)%n;
}
return start;
}
int main()
{
struct petrolPump arr[] = {{6, 4}, {3, 6}, {7, 3}};
int n = sizeof(arr)/sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1)? printf("No solution"): printf("Start = %d", start);
return 0;
}
|
Java
public class Petrol
{
static class petrolPump
{
int petrol;
int distance;
public petrolPump(int petrol, int distance)
{
this.petrol = petrol;
this.distance = distance;
}
}
static int printTour(petrolPump arr[], int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol - arr[start].distance;
while(end != start || curr_petrol < 0)
{
while(curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1) % n;
if(start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1)%n;
}
return start;
}
public static void main(String[] args)
{
petrolPump[] arr = {new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3)};
int start = printTour(arr, arr.length);
System.out.println(start == -1 ? "No Solution" : "Start = " + start);
}
}
|
Python
def printTour(arr,n):
start = 0
s = 0
d = 0
for i in range(n):
s += arr[i][0] - arr[i][1]
if s < 0:
start = i+1
d += s
s = 0
return start if (s+d)>=0 else -1
arr = [[6,4], [3,6], [7,3]]
start = printTour(arr,3)
if start == -1:
print("No Solution Possible !!!")
else:
print("start = {}".format(start))
|
C#
using System;
class GFG
{
public class petrolPump
{
public int petrol;
public int distance;
public petrolPump(int petrol,
int distance)
{
this.petrol = petrol;
this.distance = distance;
}
}
public static int printTour(petrolPump[] arr,
int n)
{
int start = 0;
int end = 1;
int curr_petrol = arr[start].petrol -
arr[start].distance;
while (end != start || curr_petrol < 0)
{
while (curr_petrol < 0 && start != end)
{
curr_petrol -= arr[start].petrol -
arr[start].distance;
start = (start + 1) % n;
if (start == 0)
{
return -1;
}
}
curr_petrol += arr[end].petrol -
arr[end].distance;
end = (end + 1) % n;
}
return start;
}
public static void Main(string[] args)
{
petrolPump[] arr = new petrolPump[]
{
new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3)
};
int start = printTour(arr, arr.Length);
Console.WriteLine(start == -1 ? "No Solution" :
"Start = " + start);
}
}
|
Javascript
<script>
class petrolPump {
constructor(petrol, distance) {
this.petrol = petrol;
this.distance = distance;
}
};
const printTour = (arr, n) => {
let start = 0;
let end = 1;
let curr_petrol = arr[start].petrol - arr[start].distance;
while (end != start || curr_petrol < 0) {
while (curr_petrol < 0 && start != end) {
curr_petrol -= arr[start].petrol - arr[start].distance;
start = (start + 1) % n;
if (start == 0)
return -1;
}
curr_petrol += arr[end].petrol - arr[end].distance;
end = (end + 1) % n;
}
return start;
}
let arr = [new petrolPump(6, 4), new petrolPump(3, 6), new petrolPump(7, 3)];
let n = arr.length;
let start = printTour(arr, n);
(start == -1) ? document.write("No solution") : document.write(`Start = ${start}`);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
First Circular Tour by checking only possible valid Starting Positions:
Another efficient solution can be to find out the first petrol pump where the amount of petrol is greater than or equal to the distance to be covered to reach the next petrol pump.
Mark that petrol pump as start and check whether we can finish the journey towards the end point.
- If in the middle, at any petrol pump, the amount of petrol is less than the distance to be covered to reach the next petrol pump, then we can say we cannot complete the circular tour from start.
- Find the next start petrol pump where the amount of petrol is greater than or equal to the distance to be covered and we mark it as start. Continue this process till all points are visited or a starting point is found.
Let us discuss why we need not look at any petrol pump in between the initial petrol pump marked as start and the new start.
Let us consider there was a petrol pump at kth position between the old start and new start. This petrol pump will break the range into two parts. The case is that
- both the parts can have negative sum,
- the starting partition can have a negative sum or
- the later half has a negative sum.
In the first and the last case we will not be able to reach the new start point.
And for the second case though we will be able to reach the new start but will not be able to complete the tour because we will not be able to cover some part in between 0 to the kth position. [As we already found that we could not reach to start from 0 and also we are not able to reach k from start. So the tour cannot be completed]
Follow the steps mentioned below to implement the idea:
- Find the first possible petrol pump where the amount of petrol is greater than the distance to the next petrol pump.
- Traverse from i = start to N:
- If the amount of petrol becomes inefficient (i.e., negative) we need to update the new start point.
- Traverse from i+1 to N and find the point where petrol is greater than the distance to the next petrol pump.
- Start from the new start point and continue the above procedure.
- Start from 0 to the found start point. If the sum of the petrol is non-negative then the start point is feasible otherwise not.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump {
public:
int petrol;
int distance;
};
int printTour(petrolPump arr[], int n)
{
int start;
for (int i = 0; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
break;
}
}
int curr_petrol = 0;
int i;
for (i = start; i < n;) {
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (int j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
int main()
{
petrolPump arr[] = { { 6, 4 }, { 3, 6 }, { 7, 3 } };
int n = sizeof(arr) / sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1) ? cout << "No solution"
: cout << "Start = " << start;
return 0;
}
|
C
#include <stdio.h>
struct petrolPump {
int petrol;
int distance;
};
int printTour(struct petrolPump arr[], int n)
{
int start;
for (int i = 0; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
break;
}
}
int curr_petrol = 0;
int i;
for (i = start; i < n;) {
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break;
}
}
}
else
{
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (int j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
int main()
{
struct petrolPump arr[]
= { { 6, 4 }, { 3, 6 }, { 7, 3 } };
int n = sizeof(arr) / sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1) ? printf("No solution")
: printf("Start = %d", start);
return 0;
}
|
Java
public class Circular
{
static class petrolPump {
int petrol;
int distance;
public petrolPump(int petrol, int distance)
{
this.petrol = petrol;
this.distance = distance;
}
}
static int printTour(petrolPump arr[], int n)
{
int start = 0;
for (int i = 0; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
break;
}
}
int curr_petrol = 0;
int i;
for (i = start; i < n;) {
curr_petrol
+= (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (int j = 0; j < start; j++) {
curr_petrol
+= (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
public static void main(String[] args)
{
petrolPump arr[]
= { new petrolPump(6, 4), new petrolPump(3, 6),
new petrolPump(7, 3) };
int n = arr.length;
int start = printTour(arr, n);
System.out.println(start == -1
? "No solution"
: "Start = " + start);
}
}
|
Python3
class petrolPump:
def __init__(self, petrol, distance):
self.petrol = petrol
self.distance = distance
def printTour(arr, n):
start = 0
for i in range(n):
if arr[i].petrol >= arr[i].distance:
start = i
break
curr_petrol = 0
for i in range(start, n):
curr_petrol += (arr[i].petrol - arr[i].distance)
if(curr_petrol < 0):
i += 1
while(i < n):
if(arr[i].petrol >= arr[i].distance):
start = i
curr_petrol = 0
break
i += 1
else:
i += 1
if(curr_petrol < 0):
return -1
for i in range(start):
curr_petrol += (arr[i].petrol - arr[i].distance)
if(curr_petrol < 0):
return -1
return start
arr = [petrolPump(6, 4), petrolPump(3, 6), petrolPump(7, 3)]
start = printTour(arr, len(arr))
if start == -1:
print("No solution")
else:
print("Start = {}".format(start))
|
C#
using System;
public class Circular {
public class petrolPump {
public int petrol;
public int distance;
public petrolPump(int petrol, int distance) {
this.petrol = petrol;
this.distance = distance;
}
}
static int printTour(petrolPump []arr, int n) {
int start = 0;
int i;
for ( i = 0; i < n; i++)
{
if (arr[i].petrol >= arr[i].distance) {
start = i;
break;
}
}
int curr_petrol = 0;
for (i = start; i < n;) {
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (int j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
public static void Main(String[] args) {
petrolPump []arr = { new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3) };
int n = arr.Length;
int start = printTour(arr, n);
Console.WriteLine(start == -1 ? "No solution" : "Start = " + start);
}
}
|
Javascript
<script>
class petrolPump {
constructor(petrol, distance) {
this.petrol = petrol;
this.distance = distance;
}
};
const printTour = (arr, n) => {
let start;
for (let i = 0; i < n; i++)
{
if (arr[i].petrol >= arr[i].distance) {
start = i;
break;
}
}
let curr_petrol = 0;
let i;
for (i = start; i < n;)
{
curr_petrol += (arr[i].petrol - arr[i].distance);
if (curr_petrol < 0) {
i++;
for (; i < n; i++) {
if (arr[i].petrol >= arr[i].distance) {
start = i;
curr_petrol = 0;
break;
}
}
}
else {
i++;
}
}
if (curr_petrol < 0) {
return -1;
}
for (let j = 0; j < start; j++) {
curr_petrol += (arr[j].petrol - arr[j].distance);
if (curr_petrol < 0) {
return -1;
}
}
return start;
}
let arr = [new petrolPump(6, 4), new petrolPump(3, 6), new petrolPump(7, 3)];
let n = arr.length;
let start = printTour(arr, n);
(start == -1) ? document.write("No solution") : document.write(`Start = ${start}`);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
First Circular Tour by using Single Loop:
The idea is similar to the above approach.
Here we will use another variable to substitute the extra loop from start till the latest found start point. The variable will store the sum of utilized petrol from 0 till the latest start petrol pump.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump {
public:
int petrol;
int distance;
};
int printTour(petrolPump p[], int n)
{
int start = 0, deficit = 0;
int capacity = 0;
for (int i = 0; i < n; i++) {
capacity += p[i].petrol - p[i].distance;
if (capacity < 0) {
start = i + 1;
deficit += capacity;
capacity = 0;
}
}
return (capacity + deficit >= 0) ? start : -1;
}
int main()
{
petrolPump arr[] = { { 6, 4 }, { 3, 6 }, { 7, 3 } };
int n = sizeof(arr) / sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1) ? cout << "No solution"
: cout << "Start = " << start;
return 0;
}
|
Java
import java.util.*;
class GFG {
static class petrolPump {
int petrol;
int distance;
petrolPump(int a, int b) {
this.petrol = a;
this.distance = b;
}
};
static int printTour(petrolPump p[], int n)
{
int start = 0, deficit = 0;
int capacity = 0;
for (int i = 0; i < n; i++) {
capacity += p[i].petrol - p[i].distance;
if (capacity < 0) {
start = i + 1;
deficit += capacity;
capacity = 0;
}
}
return (capacity + deficit >= 0) ? start : -1;
}
public static void main(String[] args) {
petrolPump arr[] = { new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3) };
int n = arr.length;
int start = printTour(arr, n);
if (start == -1)
System.out.print("No solution");
else
System.out.print("Start = " + start);
}
}
|
Python3
class petrolPump:
def __init__(self,a, b):
self.petrol = a;
self.distance = b;
def printTour( p, n):
start = 0;
deficit = 0;
capacity = 0;
for i in range(n):
capacity += p[i].petrol - p[i].distance;
if (capacity < 0):
start = i + 1;
deficit += capacity;
capacity = 0;
if(capacity + deficit >= 0):
return start;
else:
return -1;
if __name__ == '__main__':
arr = [petrolPump(6, 4),petrolPump(3, 6),petrolPump(7, 3)] ;
n = len(arr);
start = printTour(arr, n);
if (start == -1):
print("No solution");
else:
print("Start = " , start);
|
C#
using System;
public class GFG {
public class petrolPump {
public int petrol;
public int distance;
public petrolPump(int a, int b) {
this.petrol = a;
this.distance = b;
}
};
static int printTour(petrolPump []p, int n) {
int start = 0, deficit = 0;
int capacity = 0;
for (int i = 0; i < n; i++) {
capacity += p[i].petrol - p[i].distance;
if (capacity < 0)
{
start = i + 1;
deficit += capacity;
capacity = 0;
}
}
return (capacity + deficit >= 0) ? start : -1;
}
public static void Main(String[] args)
{
petrolPump []arr = { new petrolPump(6, 4),
new petrolPump(3, 6),
new petrolPump(7, 3) };
int n = arr.Length;
int start = printTour(arr, n);
if (start == -1)
Console.Write("No solution");
else
Console.Write("Start = " + start);
}
}
|
Javascript
<script>
class petrolPump {
constructor(a , b) {
this.petrol = a;
this.distance = b;
}
}
function printTour( p , n) {
var start = 0, deficit = 0;
var capacity = 0;
for (i = 0; i < n; i++) {
capacity += p[i].petrol - p[i].distance;
if (capacity < 0) {
start = i + 1;
deficit += capacity;
capacity = 0;
}
}
return (capacity + deficit >= 0) ? start : -1;
}
var arr = [ new petrolPump(6, 4), new petrolPump(3, 6), new petrolPump(7, 3) ];
var n = arr.length;
var start = printTour(arr, n);
if (start == -1)
document.write("No solution");
else
document.write("Start = " + start);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
First Circular Tour using dynamic programming
In this approach first, we will storing the difference between petrol and distance then prefix array will store the difference of petrol and distance till the i’th position and suffix array will do the same from end. The idea behind this approach is we are checking if the i’th position is suitable candidate for a starting point or not. For checking this we are storing the capacity from front and from end.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class petrolPump {
public:
int petrol;
int distance;
};
int printTour(petrolPump p[], int n)
{
vector<int> v;
for(int i=0;i<n;i++)
{
v.push_back(p[i].petrol-p[i].distance);
}
vector<int> pref(n);
pref[0]=v[0];
for(int i=0;i<n;i++)
{
pref[i]=pref[i-1]+v[i];
}
vector<int> suff(n);
suff[n-1]=v[n-1];
for(int i=n-2;i>=0;i--)
{
suff[i]=suff[i+1]+v[i];
}
int flag=0;
int ans=-1;
for(int i=0;i<n;i++)
{
if((ans==-1 && pref[i]<0) || (ans!=-1 && pref[i]-pref[ans-1]<0))
{
ans=i+1;
}
}
if(ans==-1)
{
return 0;
}
else if(ans<n)
{
if(pref[ans-1]+suff[ans]>=0)
{
return ans;
}
}
else if(ans==n)
{
if(suff[ans-1]+pref[ans-2]>=0)
{
return n-1;
}
}
return -1;
}
int main()
{
petrolPump arr[] = { { 6, 4 }, { 3, 6 }, { 7, 3 } };
int n = sizeof(arr) / sizeof(arr[0]);
int start = printTour(arr, n);
(start == -1) ? cout << "No solution"
: cout << "Start = " << start;
return 0;
}
|
Java
import java.util.*;
class GFG {
public static void main(String[] args)
{
petrolPump[] arr
= { new petrolPump(6, 4), new petrolPump(3, 6),
new petrolPump(7, 3) };
int n = arr.length;
int start = printTour(arr, n);
if (start == -1)
System.out.println("No solution");
else
System.out.println("Start = " + start);
}
static class petrolPump {
public int petrol, distance;
public petrolPump(int petrol, int distance)
{
this.petrol = petrol;
this.distance = distance;
}
}
static int printTour(petrolPump[] p, int n)
{
List<Integer> v = new ArrayList<Integer>();
for (int i = 0; i < n; i++) {
v.add(p[i].petrol - p[i].distance);
}
int[] pref = new int[n];
pref[0] = v.get(0);
for (int i = 1; i < n; i++) {
pref[i] = pref[i - 1] + v.get(i);
}
int[] suff = new int[n];
suff[n - 1] = v.get(n - 1);
for (int i = n - 2; i >= 0; i--) {
suff[i] = suff[i + 1] + v.get(i);
}
int flag = 0;
int ans = -1;
for (int i = 0; i < n; i++) {
if ((ans == -1 && pref[i] < 0)
|| (ans != -1
&& pref[i] - pref[ans - 1] < 0)) {
ans = i + 1;
}
}
if (ans == -1) {
return 0;
}
else if (ans < n) {
if (pref[ans - 1] + suff[ans] >= 0) {
return ans;
}
}
else if (ans == n) {
if (suff[ans - 1] + pref[ans - 2] >= 0) {
return n - 1;
}
}
return -1;
}
}
|
Python3
class petrolPump:
def __init__(self,a, b):
self.petrol = a;
self.distance = b;
def printTour( p, n):
v=[];
for i in range(0,n):
v.append(p[i].petrol-p[i].distance);
pref=[0]*(n);
pref[0]=v[0];
for i in range(0,n):
pref[i]=pref[i-1]+v[i];
suff=[0]*n;
suff[n-1]=v[n-1];
for i in range(n-2,-1):
suff[i]=suff[i+1]+v[i];
flag=0;
ans=-1;
for i in range(0,n):
if((ans==-1 and pref[i]<0) or (ans!=-1 and pref[i]-pref[ans-1]<0)):
ans=i+1;
if(ans==-1):
return 0;
elif(ans<n):
if(pref[ans-1]+suff[ans]>=0):
return ans;
elif(ans==n):
if(suff[ans-1]+pref[ans-2]>=0):
return n-1;
return -1;
if __name__ == '__main__':
arr = [petrolPump(6, 4),petrolPump(3, 6),petrolPump(7, 3)] ;
n = len(arr);
start = printTour(arr, n);
if (start == -1):
print("No solution");
else:
print("Start = " , start);
|
C#
using System;
using System.Linq;
using System.Collections.Generic;
class GFG
{
class petrolPump {
public int petrol, distance;
public petrolPump(int petrol, int distance)
{
this.petrol=petrol;
this.distance=distance;
}
}
static int printTour(petrolPump[] p, int n)
{
List<int> v=new List<int>();
for(int i=0;i<n;i++)
{
v.Add(p[i].petrol-p[i].distance);
}
int[] pref=new int[n];
pref[0]=v[0];
for(int i=1;i<n;i++)
{
pref[i]=pref[i-1]+v[i];
}
int[] suff=new int[n];
suff[n-1]=v[n-1];
for(int i=n-2;i>=0;i--)
{
suff[i]=suff[i+1]+v[i];
}
int flag=0;
int ans=-1;
for(int i=0;i<n;i++)
{
if((ans==-1 && pref[i]<0) || (ans!=-1 && pref[i]-pref[ans-1]<0))
{
ans=i+1;
}
}
if(ans==-1)
{
return 0;
}
else if(ans<n)
{
if(pref[ans-1]+suff[ans]>=0)
{
return ans;
}
}
else if(ans==n)
{
if(suff[ans-1]+pref[ans-2]>=0)
{
return n-1;
}
}
return -1;
}
static public void Main()
{
petrolPump[] arr = { new petrolPump(6, 4 ), new petrolPump( 3, 6 ), new petrolPump( 7, 3 ) };
;
int n = arr.Length;
int start = printTour(arr, n);
if (start == -1)
Console.Write("No solution");
else
Console.Write("Start = " + start);
}
}
|
Javascript
class petrolPump {
constructor(petrol,distance)
{
this.petrol=petrol;
this.distance=distance;
}
}
function printTour( p, n)
{
let v=[];
for(let i=0;i<n;i++)
{
v.push(p[i].petrol-p[i].distance);
}
let pref=new Array(n);
pref[0]=v[0];
for(let i=1;i<n;i++)
{
pref[i]=pref[i-1]+v[i];
}
let suff=new Array(n);
suff[n-1]=v[n-1];
for(let i=n-2;i>=0;i--)
{
suff[i]=suff[i+1]+v[i];
}
let flag=0;
let ans=-1;
for(let i=0;i<n;i++)
{
if((ans==-1 && pref[i]<0) || (ans!=-1 && pref[i]-pref[ans-1]<0))
{
ans=i+1;
}
}
if(ans==-1)
{
return 0;
}
else if(ans<n)
{
if(pref[ans-1]+suff[ans]>=0)
{
return ans;
}
}
else if(ans==n)
{
if(suff[ans-1]+pref[ans-2]>=0)
{
return n-1;
}
}
return -1;
}
let arr = [ new petrolPump(6, 4 ), new petrolPump( 3, 6 ), new petrolPump( 7, 3 ) ];
let n = arr.length;
let start = printTour(arr, n);
(start == -1) ? document.write("No solution")
: document.write("Start = " + start);
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Please Login to comment...