Largest Derangement of a Sequence

Last Updated : 22 Dec, 2022

Given any sequence, find the largest derangement of .
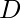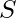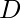A derangement $D$ is any permutation of, such that no two elements at the same position in $S$ and $D$ are equal.
The Largest Derangement is such that.

Examples:

Input : seq[] = {5, 4, 3, 2, 1}
Output : 4 5 2 1 3

Input : seq[] = {56, 21, 42, 67, 23, 74}
Output : 74, 67, 56, 42, 21, 23

Since we are interested in generating the largest derangement, we start putting larger elements in more significant positions.
Start from left, at any position 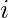$i$ place the next largest element among the values of the sequence which have not yet been placed in positions before.
To scan all positions takes N iteration. In each iteration we are required to find a maximum number, so a trivial implementation would be 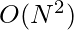$O(N^2)$ complexity,
However, if we use a data structure like max-heap to find the maximum element, then the complexity reduces to 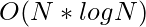$O(N * log{N})$

Below is the implementation.

C++

// C++ program to find the largest derangement
#include <bits/stdc++.h>
using namespace std;
 
void printLargest(int seq[], int N)
{
    int res[N]; // Stores result
 
    // Insert all elements into a priority queue
    std::priority_queue<int> pq; 
    for (int i = 0; i < N; i++) 
        pq.push(seq[i]);    
 
    // Fill Up res[] from left to right
    for (int i = 0; i < N; i++) {
        int d = pq.top();
        pq.pop();
        if (d != seq[i] || i == N - 1) {
            res[i] = d;
        } else {
 
            // New Element popped equals the element 
            // in original sequence. Get the next
            // largest element
            res[i] = pq.top();
            pq.pop();
            pq.push(d);
        }
    }
 
    // If given sequence is in descending order then 
    // we need to swap last two elements again
    if (res[N - 1] == seq[N - 1]) {
        res[N - 1] = res[N - 2];
        res[N - 2] = seq[N - 1];
    }
 
    printf("\nLargest Derangement \n");
    for (int i = 0; i < N; i++) 
        printf("%d ", res[i]);
}
 
// Driver code
int main()
{
    int seq[] = { 92, 3, 52, 13, 2, 31, 1 }; 
    int n = sizeof(seq)/sizeof(seq[0]);
    printLargest(seq, n);
    return 0;
}

Java

// Java program to find the largest derangement
import java.io.*;
import java.util.Collections;
import java.util.PriorityQueue;
 
class GFG{
     
public static void printLargest(int a[],int n)
{
     PriorityQueue<Integer> pq = new PriorityQueue<>(
         Collections.reverseOrder());
       
      // Insert all elements into a priority queue
      for(int i = 0; i < n; i++)
    {
        pq.add(a[i]);
    }
     
    // Stores result
      int res[] = new int[n]; 
       
      // Fill Up res[] from left to right
    for(int i = 0; i < n; i++)
    {
        int p = pq.peek();
        pq.remove();
         
        if (p != a[i] || i == n - 1)
        {
            res[i] = p;
        }
        else
        {
             
            // New Element popped equals the element 
            // in original sequence. Get the next
            // largest element
            res[i] = pq.peek();
            pq.remove();
            pq.add(p);
        }
    }
     
      // If given sequence is in descending 
      // order then we need to swap last two
      // elements again
      if (res[n - 1] == a[n - 1])
    {
        res[n - 1] = res[n - 2];
        res[n - 2] = a[n - 1];
    }
   
      System.out.println("Largest Derangement");
    for(int i = 0; i < n; i++)
    {
        System.out.print(res[i] + " ");
    }
}
 
// Driver code
public static void main(String[] args) 
{
      int n = 7;
    int seq[] = { 92, 3, 52, 13, 2, 31, 1 };
     
      printLargest(seq, n);
}
}
 
// This code is contributed by aditya7409

Python3

# Python3 program to find the largest derangement
def printLargest(seq, N) :
 
    res = [0]*N # Stores result
   
    # Insert all elements into a priority queue
    pq = []
    for i in range(N) :
        pq.append(seq[i])   
   
    # Fill Up res[] from left to right
    for i in range(N) :    
        pq.sort()
        pq.reverse()
        d = pq[0]
        del pq[0]
        if (d != seq[i] or i == N - 1) :
            res[i] = d        
        else :        
   
            # New Element popped equals the element 
            # in original sequence. Get the next
            # largest element
            res[i] = pq[0]
            del pq[0]
            pq.append(d)
   
    # If given sequence is in descending order then 
    # we need to swap last two elements again
    if (res[N - 1] == seq[N - 1]) :    
        res[N - 1] = res[N - 2]
        res[N - 2] = seq[N - 1]
          
    print("Largest Derangement")
    for i in range(N) :
        print(res[i], end = " ")
 
# Driver code
seq = [ 92, 3, 52, 13, 2, 31, 1 ] 
n = len(seq)
printLargest(seq, n)
 
# This code is contributed by divyesh072019.

C#

// C# program to find the largest derangement
using System;
using System.Collections.Generic;
class GFG 
{
     
    static void printLargest(int[] seq, int N)
    {
        int[] res = new int[N]; // Stores result
      
        // Insert all elements into a priority queue
        List<int> pq = new List<int>();
        for (int i = 0; i < N; i++) 
            pq.Add(seq[i]);    
      
        // Fill Up res[] from left to right
        for (int i = 0; i < N; i++) 
        {
            pq.Sort();
            pq.Reverse();
            int d = pq[0];
            pq.RemoveAt(0);
            if (d != seq[i] || i == N - 1) 
            {
                res[i] = d;
            } 
          else
            {
      
                // New Element popped equals the element 
                // in original sequence. Get the next
                // largest element
                res[i] = pq[0];
                pq.RemoveAt(0);
                pq.Add(d);
            }
        }
      
        // If given sequence is in descending order then 
        // we need to swap last two elements again
        if (res[N - 1] == seq[N - 1]) 
        {
            res[N - 1] = res[N - 2];
            res[N - 2] = seq[N - 1];
        }     
        Console.WriteLine("Largest Derangement");
        for (int i = 0; i < N; i++) 
            Console.Write(res[i] + " ");
    }
 
  // Driver code
  static void Main()
  {
    int[] seq = { 92, 3, 52, 13, 2, 31, 1 }; 
    int n = seq.Length;
    printLargest(seq, n);
  }
}
 
// This code is contributed by divyeshrabadiya07

Javascript

<script>
 
// JavaScript program to find the largest derangement
 
 
function printLargest(seq, N) {
    let res = new Array(N); // Stores result
 
    // Insert all elements into a priority queue
    let pq = new Array();
    for (let i = 0; i < N; i++)
        pq.push(seq[i]);
 
    // Fill Up res[] from left to right
    for (let i = 0; i < N; i++) {
        pq.sort((a, b) => a - b);
        pq.reverse();
        let d = pq[0];
        pq.shift();
        if (d != seq[i] || i == N - 1) {
            res[i] = d;
        }
        else {
 
            // New Element popped equals the element
            // in original sequence. Get the next
            // largest element
            res[i] = pq[0];
            pq.shift();
            pq.push(d);
        }
    }
 
    // If given sequence is in descending order then
    // we need to swap last two elements again
    if (res[N - 1] == seq[N - 1]) {
        res[N - 1] = res[N - 2];
        res[N - 2] = seq[N - 1];
    }
    document.write("Largest Derangement<br>");
    for (let i = 0; i < N; i++)
        document.write(res[i] + " ");
}
 
// Driver code
let seq = [92, 3, 52, 13, 2, 31, 1];
let n = seq.length;
printLargest(seq, n);
 
// This code is contributed by gfgking
 
</script>

Output

Largest Derangement 
52 92 31 3 13 1 2

Time Complexity: O(n log n)
Auxiliary Space: O(N), because, we use an N size array to store results.

Note:

The method can be easily modified to obtain the smallest derangement as well.
Instead of a Max Heap, we should use a Min Heap to consecutively get minimum elements