Open In App

Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction)

Last Updated : 28 Jun, 2022
Improve
Improve
Like Article
Like
Save
Share
Report

A matching in a Bipartite Graph is a set of the edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matching for a given Bipartite Graph.

We have discussed importance of maximum matching and Ford Fulkerson Based approach for maximal Bipartite Matching in previous post. Time complexity of the Ford Fulkerson based algorithm is O(V x E). Hopcroft Karp algorithm is an improvement that runs in O(√V x E) time. Let us define few terms before we discuss the algorithm 

Free Node or Vertex: Given a matching M, a node that is not part of matching is called free node. Initially all vertices as free (See first graph of below diagram). In second graph, u2 and v2 are free. In third graph, no vertex is free. 

Matching and Not-Matching edges: Given a matching M, edges that are part of matching are called Matching edges and edges that are not part of M (or connect free nodes) are called Not-Matching edges. In first graph, all edges are non-matching. In second graph, (u0, v1), (u1, v0) and (u3, v3) are matching and others not-matching. 

Alternating Paths: Given a matching M, an alternating path is a path in which the edges belong alternatively to the matching and not matching. All single edges paths are alternating paths. Examples of alternating paths in middle graph are u0-v1-u2 and u2-v1-u0-v2. 

Augmenting path: Given a matching M, an augmenting path is an alternating path that starts from and ends on free vertices. All single edge paths that start and end with free vertices are augmenting paths. In below diagram, augmenting paths are highlighted with blue color. Note that the augmenting path always has one extra matching edge. The Hopcroft Karp algorithm is based on below concept. A matching M is not maximum if there exists an augmenting path. It is also true other way, i.e, a matching is maximum if no augmenting path exists So the idea is to one by one look for augmenting paths. And add the found paths to current matching. 

Hopcroft Karp Algorithm:

  1. Initialize Maximal Matching M as empty.
  2. While there exists an Augmenting Path p
    • Remove matching edges of p from M and add not-matching edges of p to M
    • (This increases size of M by 1 as p starts and ends with a free vertex)
  3. Return M. 

Below diagram shows working of the algorithm.

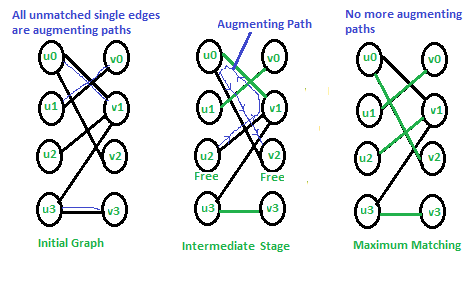
 HopcroftKarp 

In the initial graph all single edges are augmenting paths and we can pick in any order. In the middle stage, there is only one augmenting path. We remove matching edges of this path from M and add not-matching edges. In final matching, there are no augmenting paths so the matching is maximum. 

Implementation of Hopcroft Karp algorithm is discussed in set 2. 
Hopcroft–Karp Algorithm for Maximum Matching | Set 2 (Implementation) 


https://media.geeksforgeeks.org/auth/avatar.png
GeeksforGeeks
Improve
Previous Article
Boggle (Find all possible words in a board of characters) | Set 1
Next Article
Construct a graph from given degrees of all vertices

Similar Reads

Hopcroft–Karp Algorithm for Maximum Matching | Set 2 (Implementation)
We strongly recommend to refer below post as a prerequisite.Hopcroft–Karp Algorithm for Maximum Matching | Set 1 (Introduction) There are few important things to note before we start implementation. We need to find an augmenting path (A path that alternates between matching and not matching edges and has free vertices as starting and ending points)
13 min read
Hopcroft–Karp Algorithm in Python
A matching in a Bipartite Graph is a set of edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matching for a given Bipartite Graph. Hopcroft Karp
5 min read
Rabin-Karp algorithm for Pattern Searching in Matrix
Given matrices txt[][] of dimensions m1 x m2 and pattern pat[][] of dimensions n1 x n2, the task is to check whether a pattern exists in the matrix or not, and if yes then print the top most indices of the pat[][] in txt[][]. It is assumed that m1, m2 ? n1, n2 Examples: Input: txt[][] = {{G, H, I, P} {J, K, L, Q} {R, G, H, I} {S, J, K, L} } pat[][]
15+ min read
Implementing Rabin Karp Algorithm Using Rolling Hash in Java
There are so many pattern searching algorithms for the string. KMP algorithm, Z algorithm Rabin Karp algorithm, etc these algorithms are the optimization of Naive Pattern searching Algorithm. Naive Pattern Searching Algorithm: Input : "AABACACAACAC" Pattern : "CAC" Output : [4,9] AABACACAACAC Implementation: Java Code // Java Program to Search for
5 min read
Count distinct substrings of a string using Rabin Karp algorithm
Given a string, return the number of distinct substrings using Rabin Karp Algorithm. Examples: Input : str = “aba”Output : 5Explanation :Total number of distinct substring are 5 - "a", "ab", "aba", "b" ,"ba" Input : str = “abcd”Output : 10Explanation :Total number of distinct substring are 10 - "a", "ab", "abc", "abcd", "b", "bc", "bcd", "c", "cd",
9 min read
Rabin-Karp Algorithm for Pattern Searching
Given a text T[0. . .n-1] and a pattern P[0. . .m-1], write a function search(char P[], char T[]) that prints all occurrences of P[] present in T[] using Rabin Karp algorithm. You may assume that n > m. Examples: Input: T[] = "THIS IS A TEST TEXT", P[] = "TEST"Output: Pattern found at index 10 Input: T[] = "AABAACAADAABAABA", P[] = "AABA"Output:
15 min read
Karp's minimum mean (or average) weight cycle algorithm
Given a directed and strongly connected graph with non-negative edge weights. We define the mean weight of a cycle as the summation of all the edge weights of the cycle divided by the no. of edges. Our task is to find the minimum mean weight among all the directed cycles of the graph. Example: Input : Below Graph Output : 1.66667 Method to find the
11 min read
Find maximum matching in a given Binary Tree
Given a Tree with N nodes values from 1 to N and N - 1 edges. The task is to find the maximum matching in the given tree. A matching in a tree is a collection of edges such that no pair of edges share a common node. Matching with the most edges is known as a maximum matching. Examples: Input: Below is the given graph: Output: 3 Explanation: Set of
14 min read
Maximum Bipartite Matching
A matching in a Bipartite Graph is a set of the edges chosen in such a way that no two edges share an endpoint. A maximum matching is a matching of maximum size (maximum number of edges). In a maximum matching, if any edge is added to it, it is no longer a matching. There can be more than one maximum matchings for a given Bipartite Graph. Why do we
15+ min read
Longest Common Prefix Matching | Set-6
Given a set of strings, find the longest common prefix. Examples: Input: str[] = {geeksforgeeks, geeks, geek, geezer} Output: gee Input: str[] = {apple, ape, april} Output: ap Previous Approaches: Set1 | Set2 | Set3 | Set4 | Set5 Approach: Sort the given set of N strings.Compare the first and last string in the sorted array of strings.The string wi
6 min read
Article Tags :
Practice Tags :
three90RightbarBannerImg
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox